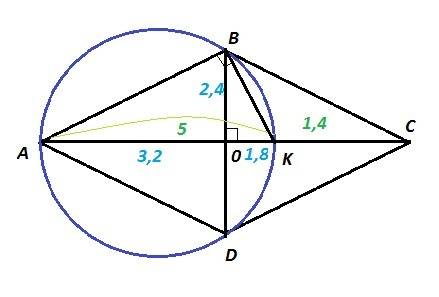
Ромб ABCD, окружность проходит через точки A, B, C
AK = 5 см; КС = 1, 4 см ⇒ АС = АК + КС = 5 + 1,4 = 6,4 см
У ромба диагонали перпендикулярны и точкой пересечения делятся пополам : AC⊥BD; AO=OC = AC/2 = 6,4 /2 = 3,2 см; BO=OD.
AK⊥BD и делит хорду BD пополам ⇒ AK - диаметр окружности.
ΔABK - прямоугольный, так как сторона AK является диаметром описанной окружности.
Высота треугольника, проведенная из прямого угла на гипотенузу, есть среднее геометрическое проекций катетов на гипотенузу :
BO² = AO·OK = AO·(AK-AO) = 3,2·(5-3,2) = 3,2·1,8 = 5,76 = 2,4²
BO = 2,4 см
ΔAOB образован диагоналями, прямоугольный. Теорема Пифагора
AB² = AO² + BO² = 3,2²+2,4² = 10,24+5,76= 16 = 4²
AB = 4 см
ответ: сторона ромба равна 4 см
Объяснение:
1 . ABCDEF - правильний вписаний 6 - кутник ; d = AD = 10 см ;
а₆ = r = OA = 1/2 d = 1/2 * 10 = 5 ( см ) ;
P = 6 * a₆ = 6 * 5 = 30 ( см ) ; Р = 30 см .
2 . КМ - сторона правильного тр - ника , вписаного в коло ,
тому h Δ = ( a₃ √3 )/2 = ( 12√3 * √3 )/2 = ( 12 * 3 )/2 = 18 ( см ) ;
r = 2/3 *h Δ = 2/3 * 18 = 12 ( см ) ; r = 12 см ; тоді довжина L
дуги КМ буде : L = ( π r n )/180 = ( π *12 *120 )/180 = 8π ≈ 25,12 ( см ) ;
L = 8π ≈ 25,12 см .
3 . Суму кутів n - кутника обчислюють за формулою :
K = 180°( n - 2 ) .
Маємо 180°( n - 2 ) = 1800° ;
n - 2 = 1800° : 180° ;
n - 2 = 10 ;
n = 12 сторін .
Величина вписанного угла в два раза меньше центрального, опирающегося на ту же дугу.
45,2 * 2= 90,4° (величина центрального угла)