Стороны параллелограмма равны 4 см и 9 см, а угол между ними равен 120°. Чему равны диагонали параллелограмма?

👇

Открыть все ответы

Ответ:

Podokonik

17.12.2021

Дан параллелограмм ABCD На продолжении диагонали АС за вершины А и С отмечены точки М и N соответственно так, что АМ = CN Докажите, что MBND –

Доказываешь, что два треугольник AMD и CNB:АМ = CN по условию,АВ=СВ, т.к. это стороны параллелограмма.По первому признаку равенства треугольников: AMD = CNBИз того же равенства треугольников получаешь, чтоПроверенные ответы содержат наджную, заслуживающую доверия информацию, оценнную командой экспертов. На «Знаниях» вы найдте миллионы ответов, правильность которых подтвердили активные участники сообщества, но Проверенные ответы — это лучшие из лучших.

Диагональ ВD исходного параллелограмма АВСD осталась прежней, диагональACс каждой стороны увеличилась на одинаковую длину. Точка пересечения диагонали ВD и диагоналиМNосталась прежней и делит их, как и в исходном четырехугольнике, пополам.
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то такой четырехугольник параллелограмм.

4,4(62 оценок)

Ответ:

sasharyabukhina

17.12.2021

1. Угол между боковым ребром и плоскостью основания пирамиды равен 45°.

2. Объем пирамиды равен 24 ед.³

Объяснение:

Требуется найти:

1. Угол между боковым ребром и плоскостью основания пирамиды.

2. Объем пирамиды.

476.

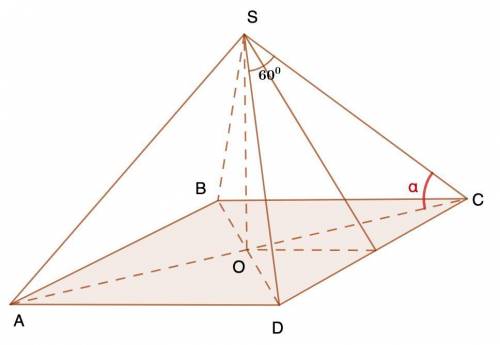
Дано: SABCD - правильная пирамида.

∠DSC - 60°;

Найти: ∠SCO.

В основании правильной четырехугольной пирамиды лежит квадрат, а боковые грани - равнобедренные треугольники.

1. Рассмотрим ΔDSC - равнобедренный.

Углы при основании равнобедренного треугольника равны.

∠DSC = 60° ⇒ ∠SDC = ∠SCD = (180° - 60°) : 2 = 60°

⇒ ΔDSC - равносторонний.

⇒ Все ребра пирамиды равны.

Пусть ребро пирамиды равно а.

2. Рассмотрим ΔАСD - прямоугольный.

По теореме Пифагора:

AC² = AD² + DC²

AC = a√2

Диагонали квадрата точкой пересечения делятся пополам.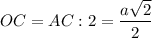

⇒ $\displaystyle OC=AC:2=\frac{a\sqrt{2} }{2}$

3. Рассмотрим ΔОSC - прямоугольный.

Пусть ∠SCO = α

Косинус угла равен отношению прилежащего катета к гипотенузе.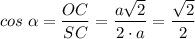

$\displaystyle cos\;\alpha =\frac{OC}{SC} =\frac{a\sqrt{2} }{2\cdot {a}} =\frac{\sqrt{2} }{2}$

⇒ α = 45°

Угол SCO равен 45°.

486.

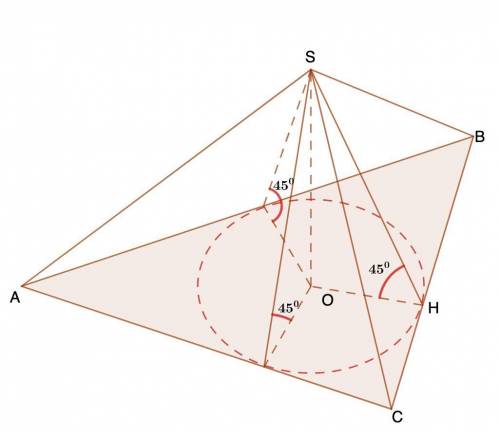
Дано: SABC - пирамида;

ВС = 9; АС = 10; АВ = 17;

Грани составляют с плоскостью основания углы в 45°.

Найти: V пирамиды.

Если боковые грани пирамиды наклонены к плоскости основания под одинаковым углом, то высота, опущенная из вершины на основание, падает в центр вписанной в основание окружности.

Объем пирамиды равен:

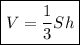$\displaystyle \boxed { V=\frac{1}{3}Sh }$ , где S - площадь основания, h - высота пирамиды.

1. Радиус вписанной окружности найдем по формуле:

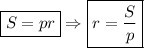$\displaystyle \boxed {S=pr} \Rightarrow \boxed{r=\frac{S}{p} }$ ,

где S - площадь треугольника, р - полупериметр.

p = (9 + 10 + 17) : 2 = 18 (ед.)

Площадь найдем по формуле Герона:

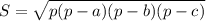$S=\sqrt{p(p-a)(p-b)(p-c)}$ , где a, b, c - стороны треугольника.

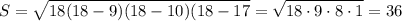$\displaystyle S=\sqrt{18(18-9)(18-10)(18-17}=\sqrt{18\cdot9\cdot8\cdot1}=36$ (ед.²)

Тогда радиус равен:

r = ОН = 36 : 18 = 2 (ед.)

2. Рассмотрим ΔОSH - прямоугольный.

Угол между боковой гранью и основанием равен двугранному углу SBCO.Двугранный угол измеряется величиной линейного угла, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.

⇒∠SHO = 45°

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠HSO = 90° - 45° = 45°

Тогда ΔОSH - равнобедренный.

⇒ ОН = SO = 2 (ед.)

3. Найдем объем:

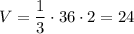$\displaystyle V=\frac{1}{3}\cdot36 \cdot2=24$ (ед.³)