
Вариант решения.
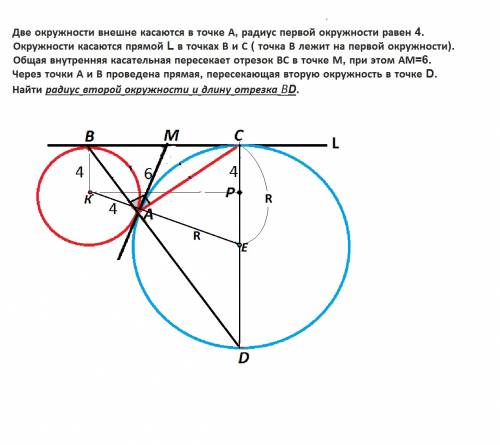
Обозначим центр меньшей окружности буквой К, центр большей - Е.
ВК и СЕ - радиусы этих окружностей.
Радиусы окружностей, проведенные к касательной в точку касания, образуют с ними прямой угол.
Отрезки касательных, проведенных к окружности из одной точки, равны. ⇒
ВМ=МА.
АМ=МС на том же основании.
Отсюда ВМ=МС=АМ=6
Следовательно, АМ - медиана треугольника ВАС.
Если медиана треугольника равна половине стороны, к которой проведена, то этот треугольник- прямоугольный.
Треугольник ВАС = прямоугольный, и его гипотенуза ВС=2АМ=12.
Проведем прямую КР параллельно прямой L
В прямоугольнике КВСР КР=ВС=12, угол КРЕ - прямой.
⇒ треугольник КРЕ - прямоугольный.
В нем катет КР=12, катет РЕ= R-4
Гипотенуза КЕ=r+R=4+R
По т. Пифагора выразим гипотенузу КЕ
КЕ²=КР²+РЕ²
(4+R)²=12²+(R-4)²
16+8R+R²=144+R²-8R+16
16 R=144
R=9
Так как угол ВАС=90°, смежный с ним угол САD=90°, и тогда хорда СD, на которую он опирается, - диаметр окружности и равна 2R=18
DВ найдем из прямоугольного треугольника ВСD.
DB²=BC²+CD²
BD²=144+324
BD=6√13
Найдем модуль вектора АМ. Для этого определим его координаты. Они равны разности координат КОНЦА и НАЧАЛА вектора. То есть АМ{9;2}. Модуль вектора равен корню квадратному из суммы квадратов его координат, то есть |AM| = √(81+4) = √85. Мы знаем, что модули векторов АМ и МС равны. Значит модуль вектора МС{(p-3);6+1)} (его координаты определяем также по разности координат КОНЦА и НАЧАЛА) равен √85. То есть (р-3)²+49=85. Решаем это квадратное уравнение и получаем, что р1=3+√36=9 и р2=-3.
ответ: C(9;6) и С(-3;6).
Смотри рисунок.