По условию данные две прямые не имеют общих точек с прямой а и пересекаются в т.М, значит, лежат в одной плоскости (свойство). Прямые в пространстве могут пересекаться, быть параллельными или скрещивающимися. Предположим, что ни одна из этих прямых не является скрещивающейся с прямой а. Так как они не пересекают прямую а ( не имеют с ней общих точек). обе параллельны прямой а. Но это допущение противоречит
Аксиоме параллельных прямых. Через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.
⇒ Данные прямые не могут обе быть параллельными прямой а, поэтому хотя бы одна из них является скрещивающейся с прямой а
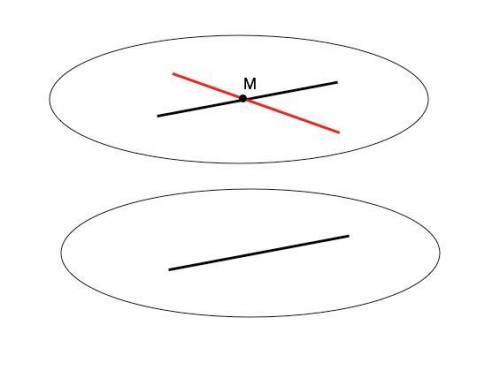
№1.
Если через точку А провести прямую, не совпадающую с прямой а, то точка А будет являться общей точкой для этих прямых, т.е. точкой их пересечения. Не пересекаются прямые, называемые параллельными, которые не имеют общих точек, в данном случае общей является точка А.
№2.
Через точку А проведём прямую а, через точку В - прямую b.
Две прямые, параллельные одной и той же прямой, параллельны между собой или совпадают. Поэтому если прямая а||l и b||l, то a||b или а=b.
№3.
Если a||b, то прямые a и b не имеют общих точек. Если прямые b и а не имеют общих точек, то b||a.
Угол равен 60°.
Объяснение:
Нужно найти угол С - угол между векторами СА и СВ.
Вектор СА{1-1;3-2;0-1} или СА{0;1;-1}.
Модуль (длина) вектора СА: |СА| = √(0+1+1) = √2.
Вектор СВ{2-1;3-2;1-1} или СВ{1;1;0}
Модуль (длина) вектора СВ: |СВ| = √(1+1+0) = √2.
Косинус угла между векторами равен скалярному произведению векторов, деленному на произведение их модулей.
CosC =(0·1 +1·1 + 1·0)/(√2·√2) = 1/2. =>
Угол C равен 60 градусов.