В треугольнике ABC проведены высота AH и медиана AM, а также средняя линия KL, параллельная стороне BC. Какой из углов больше:
угол KHL или угол KML?
Объяснение:
1) Т.к. К, М середины АВ и ВС , то КМ -средняя линия ΔАВС. По т. о средней линии треугольника КМ║АС⇒КМ║АL.
Т.к. L, М середины АC и ВС , то LМ -средняя линия ΔАВС. По т. о средней линии треугольника LМ║АB⇒LМ║АK.
Значит АLMK- параллелограмм по определению и ∠КМL=∠KAL ,по свойству противоположных углов параллелограмма .
2)Т.к. КL║BC и АН⊥ВС ⇒ КL⊥АН.
Т.к. КL средняя линия , то АО=ОН ⇒ КL- серединный перпендикуляр , каждая точка которого равноудалена от концов отрезка АН. Поэтому КА=КН и LA=LH ⇒
ΔКАН-равнобедренный : ∠КАН=∠КНА ;
ΔLAH -равнобедренный : ∠LAH=∠LHA ;
3) 
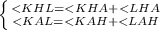⇒ ∠КHL=∠KAL ⇒ ∠КHL=∠KML Вот так неожиданно и странно.
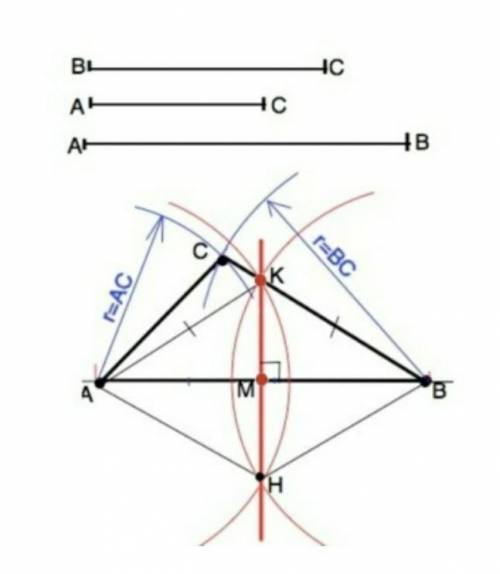
1). На произвольной прямой отложить отрезок, равный стороне АВ. Обозначить на концах отрезка вершины треугольника: точки А и В.
2) Из точки А как из центра раствором циркуля радиусом, равным длине стороны АС, начертить дугу.
3) Из т.В как из центра раствором циркуля радиусом, равным длине стороны ВС, начертить дугу до пересечения с первой дугой.
Точка пересечения дуг – вершина С искомого треугольника. Соединив А и С, В и С, получим треугольник со сторонами заданной длины.
б) Построение срединного перпендикулярна стандартное.
Из т.А и т.В как из центров провести полуокружности произвольного, но равного радиуса несколько больше половины АВ так, чтобы они пересеклись по обе стороны от АВ (т.К и т. Н).
Точки пересечения К и Н этих полуокружностей соединить.
Соединить А и Н, В и Н. Четырехугольник АКВН - ромб ( стороны равны взятому радиусу). Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. =>
АМ=МВ и КМ перпендикулярно АВ.
КМ - срединный перпендикуляр к стороне АМ.
Точно так же делят отрезок пополам.
hello, it's me, i was wondered....