Теорема.
Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, притом только один.
Доказательство:
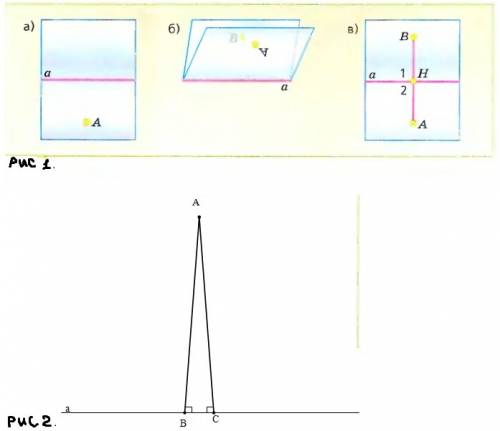
1) смотри рисунок 1
Пусть А - точка, не лежащая на данной прямой a. Докажем, что из точки А можно провести перпендикуляр к прямой a. Мысленно перегнем плоскость по прямой a так, чтобы полуплоскость с границей А, содержащая точку А, наложилась на другую полуплоскость. При этом точка A наложится на некоторую точку. Обозначим ее буквой B. Разогнем плоскость и проведем через точки A и B прямую.
Пусть H – точка пересечения прямых AB и a. При повторном перегибании плоскости по прямой a точка H останется на месте. Поэтому луч HA наложится на луч HB, и, следовательно, угол 1 совместится с углом 2. Таким образом, ∠1 = ∠2. Так как углы 1 и 2 – смежные, то их сумма равна 180°, поэтому каждый из них – прямой. Следовательно, отрезок AH – перпендикуляр к прямой a.
2) смотри рисунок 2
Допустим, что таких перпендикуляров существует два. Тогда получим треугольник ABC с двумя прямыми углами, ведь АВ и АС - перпендикулярны. Но этого быть не может. Следовательно, наше предположение о том, что через одну точку к данной прямой на плоскости можно провести больше одного перпендикуляра, - не верно и такой перпендикуляр существует только один.
1. Отрезок FK пересекает прямую РМ
2. При пересечении двух прямых, образуются смежные, а также вертикальные углы. Смежные углы это те, которые на одной прямой, а прямая у нас 180°. Поэтому, мы от 180° отнимаем известный нам угол (58°), находим смежный ему угол (122°). Остальные углы они являются вертикальными по отношению к этим. Поэтому, тот угол, который напротив угла в 58° равен 58°. А тот который напротив 122°,равен 122°.
3. K-середина отрезка CD, то следует что CK и KD равны, а значит 8:2=4см--CK, KD. CM=MK то 4:2=2см--CM,MK. ответ: CM=2cm; MK=2cm; KD=8cm.
Объяснение: