Сумма смежных углов равна 180°.
∠1 смежный с ∠2 => ∠2 = 180° - 67° = 113°
ответ: 113°.
Объяснение:
Дано:
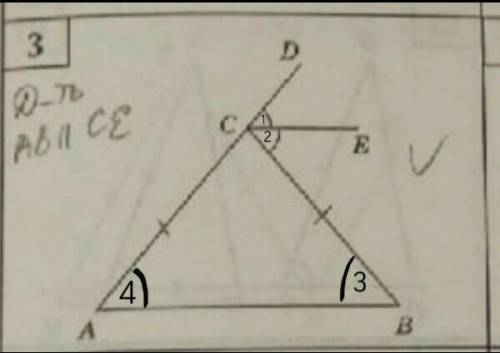
ACB - треугольник.
CE и AB - прямые, пересекающиеся секущими CA и CB.
∠ 1 = ∠ 2;
AC = CB.
Доказать:
AB || CE.
Доказательство:
Вспомним теорему: внешний угол тр-ка равен сумме двух внутренних, не смежных с ним ⇒ ∠ DCB - внешний угол,
а внутренние углы лежат на основании равнобедренного тр-ка ACB (т.к. AC = CB) и в соответствии со свойством (углы при основании в равнобедренном тр-ке равны) можно смело назвать их равными между собой (∠ 3 =∠ 4) т.е. ∠ DCB равен сумме ∠ 3 и ∠ 4 в равнобедренном тр-ке.
CE - биссектриса ∠ DCB ⇒ каждый угол при основании данного равнобедренного тр-ка равен половине внешнего угла DCB ⇒ ∠ 2 = ∠ 3, а они накрест лежащие при прямых CE и AB и секущей CB ⇒ AB || CE (по теореме: если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны)
Также можно отметить, что ∠ 1 = ∠ 4, а они соответственные при прямых CE и AB и секущей CB ⇒ AB || CE (по теореме: если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны).
Доказано!
Объяснение:
Дано:
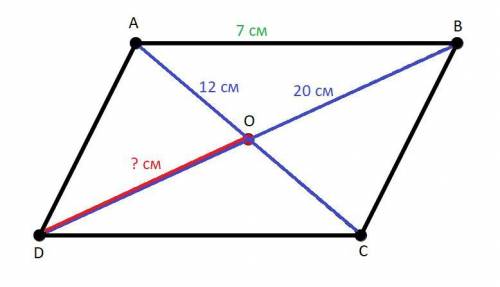
ABCD - параллелограмм.
AC и BD - диагонали параллелограмма.
AC ∩ BD = O.
AC = 12 (см); BD = 20 (см); AB = 7 (см).
Найти:
DO - ? (см).
Тут всё довольно просто. Так как ABCD - параллелограмм, вспомним свойство такой геометрической фигуры: диагонали параллелограмма точкой пересечения делятся пополам. Т.е. диагонали AC и BD делятся точкой пересечения O пополам. Соответственно DO будет равняться половине всей диагонали BD. (и из этого следует, что DO = OB)
DO = BD/2 = 20 : 2 = 10 (см)
Сумма смежных углов равна 180°.
Тогда второй угол, смежный с углом в 67° = 180°-67° = 113°.
ответ: 113°.