Конус;
Осевое сечение конуса - равнобедренный △АВС;
∠В = 120°;
АВ = ВС = 6 см.
Найти:V - ? (см³).
Решение:Проведём высоту ВН. Получилось два равных прямоугольных треугольника АВН и СВН (их равенство можно также доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что △АВС - равнобедренный).
"Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является медианой и биссектрисой".
⇒∠АВН = ∠СВН = 120°/2 = 60°, так как ВН - биссектриса.
СН/СВ = sin ∠CBH ⇒ R = CH = CB ⋅ sin 60˚ = 6 ⋅ √3/2 = 3√3 (см).
Найдём высоту ВН, по теореме Пифагора:
с = √(a² + b²) ⇒ a = √(c² - b²), где a и b - катеты, c - гипотенуза.
a = √(6² - (3√3)²) = √9 = 3 (см).
Итак, ВН = 3 (см).
V = 1/3πR²h = π(1/3 ⋅ (3√3)² ⋅ 3) = 27π (см³).
ответ: 27π (см³).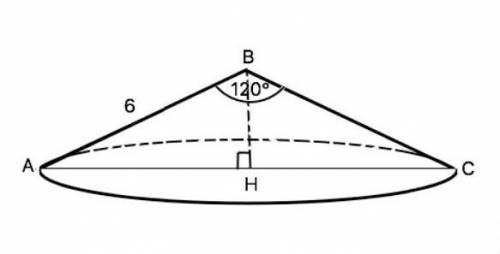
Висоти паралелограма дорівнюють 5 см і 6 см, а сума двох його суміжних сторін - 22 см. Знайдіть площу паралелограма.
Высоты параллелограмма равны 5 см и 6 см, а сумма двух его смежных сторон - 22 см. Найдите площадь параллелограмма.
Пусть длина одной из неравных сторон параллелограмма x см ;
длина другой стороны будет (22-x) см .
Можем написать уравнение x*5 =(22-x)6 || =S ||
5x =22*6 - 6x ;
5x +6x =22*6 ;
11x =22*6 ;
x = 22*6 /11= 2*6 =12 (см). [ так и должно быть x > 22/2 =11 ; 12 > 11 ]
S =x*5 = 12*5 = 60 (см²)
ответ: 60 см² .
! 5a = 6b [ очевидно a > b ] a /b = 6/5
ah₁ =bh₂ ; a/b = =h₂/ h₁ обратная пропорциональность