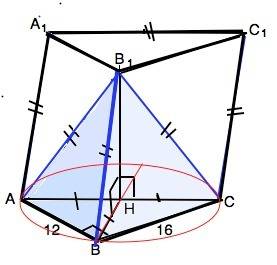
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
Найти стороны треугольника, если АМ= 9, СК= 12.
Решение:
Медианы треугольника точкой пересечения О делятся в отношении 2:1, считая от вершины.
Дано: АМ=9, СК=12. Значит АО=9*(2/3)=6, ОМ=3, СО=12*(2/3)=8, ОК=4.
В прямоугольном треугольнике АОС (угол АОС=90° - дано) гипотенуза АС по Пифагору равна АС=√(АО²+ОС²) или АС=√(6²+8²)=10.
В прямоугольном треугольнике АОК (угол АОК=90° - дано) гипотенуза АК по Пифагору равна АК=√(АО²+ОК²) или АК=√(6²+4²)=2√13. АВ=2*АК, так как СК - медиана. АВ=4√13.
В прямоугольном треугольнике СОМ (угол СОМ=90° - дано) гипотенуза СМ по Пифагору равна СМ=√(ОМ²+ОС²) или СМ=√(3²+8²)=√73. ВС=2*СМ, так как АМ - медиана. ВС=2√73.
ответ: стороны треугольника равны АС=10; АВ=4√13≈14,4; ВС=2√73≈17.
Проверка:
Три медианы делят треугольник на 6 равновеликих треугольника.
Площадь одного из них равна Saok=(1/2)*6*4=12. значит Sabc=6*12=72.
В то же время по Герону Sabc=√[p(p-a)(p-b)(p-c)], где р - полупериметр треугольника, а,b,c - его стороны. Полупериметр равен:
р=(2√73+4√13+10)/2=(√73+2√13+5).
Подставим найденные значения в формулу:
Sabc=√[(√73+(2√13+5))*(2√13+5-√73)*(√73+(5-2√13))*(√73-(5-2√13))]=
√[((2√13+5)²-73)*(73-(5-2√13)²)]=√[(52+25+20√13-73)*(73-25+20√13-52)]=
√[(20√13+4)*(20√13-4)]=√(5200-16)=72.
Итак, стороны треугольника найдены правильно.