4 квадратных сантиметра.
Объяснение:
Так как одна сторона 1 см, а вторая - 4 см.
Чтобы найти площадь прямоугольника, нужно умножить одну сторону на вторую.
Решение: 4×1=4(см квадратных)- площадь прямоугольника.
Объяснение:
Если в осевом сечении цилиндра лежит квадрат, значит, радиус основания и высота у него равны.
Зная, что гипотенуза квадрата равна 8 см, обозначаем катеты прямоугольного треугольника через Х:
По теореме Пифагора находи значение Х:
2Х2= 64;
Х2 = 32;
Х = √32.
Площадь боковой поверхности цилиндра равна произведению площади основания на высоту:
S = П * D * Н.
П = 3,14;
D и H равны √32.
Находим площадь боковой поверхности цилиндра:
S = 3,14 * √32 * √32 = 3,14 * 32 = 100,48 см2.
ответ: Площадь боковой поверхности цилиндра равна 100,48 см2
1) 
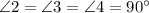; 2) Величина острого (наименьшего) угла.
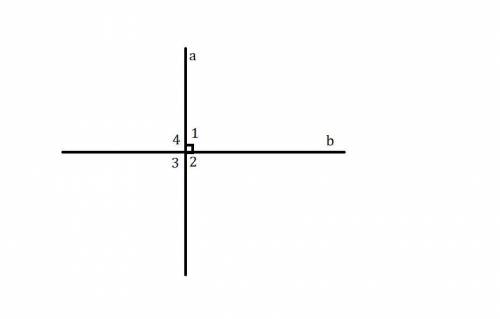
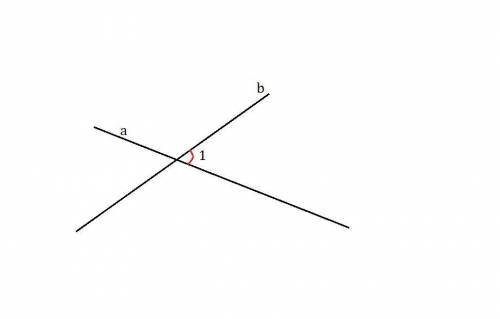
1) Начертим две пересекающие прямые. Обозначим их буквами 
и 
При их пересечении, образовался угол в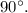 
Пусть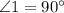 
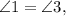как вертикальные.
.
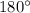и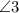 
- смежные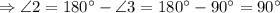 
как вертикальные.
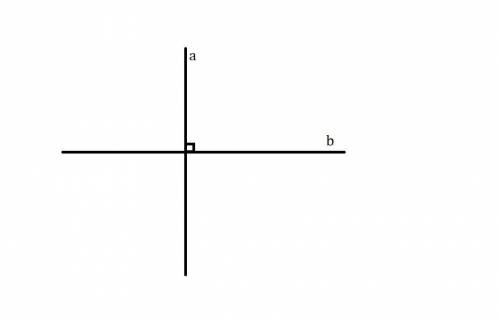
2) Угол между двумя пересекающимися прямыми - это величина наименьшего угла между двумя пересекающимися прямыми.
Обозначим две пересекающиеся прямые буквами и
При пересечении произвольных прямых, образуются 4 угла: 2 равных тупых угла и 2 равных острых угла (они равны, как вертикальные).
В данном случае наименьший угол - это величина острого угла, так как величина острого угла меньше тупого.
=============================================================
Но если прямые перпендикулярные (прямые, при пересечении которых образуются 4 прямых угла), то наименьший угол - это величина прямого. Но в данной задаче этого не уточняется, поэтому верный ответ - величина острого угла.
Восемь..............