Равнобедренный треугольник.
S = 9√3 см².
Один из углов = 120°.
Найти:Боковая сторона = ? см.
Решение:Обозначим равнобедренный треугольник буквами A, B и C.
Пусть ∠B - один из внутренних углов ΔABC, равный 120°.
Формула площади данного треугольника:
S ΔABC = 1/2 * a² * sin(B), где a - боковая сторона.
Т. к. площадь этого треугольника нам известна, приравняем данную формулу к значению площади ΔABC и решим полученное уравнение:
1/2 * a² * sin(B) = 9√3
1/2 * a² * sin(120°) = 9√3
(1/2)a² * (√3)/2 = 9√3
1/2 * ((√3)/2)a² = 9√3
((√3)/4)a² = 9√3
a² = 4 * 9
a² = 36
a = ± √36
a₁ = 6; a₂ = -6
Так как единица измерения не может быть отрицательным числом
⇒ a = 6 см.
В равнобедренном треугольнике боковые стороны равны.
⇒ AB = BC = 6 см.
ответ: 6 см.
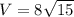
Объяснение:
(Смотри вложение)
Формула объёма пирамиды: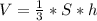 
, где:
S - площадь основания
h - высота пирамиды
Т.к. пирамида правильная ⇒ в основании лежит правильный многоугольник, то есть, в нашем случае, равносторонний треугольник
Формула площади треугольника: SΔ =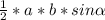 
, где
а - одна сторона
b - соседняя с а сторона
sin α - синус угла между сторонами a и b
Т.к. в основании треугольник равносторонний⇒все углы = 60° и a=b
SΔ =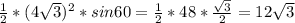 
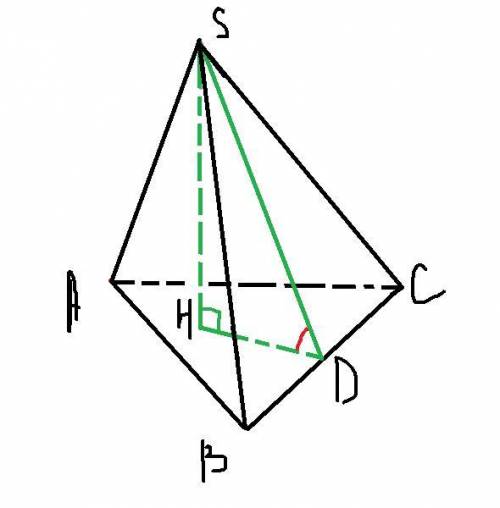
Рассмотрим ΔABC
Т.к. все треугольники равносторонние (т.к. пирамида правильная) ⇒ высота AD является также медианой и биссектрисой. Получается ∠ABC =∠ACB = 60° : 2 = 30° и BD=DC = 4√3 : 2 = 2√3
Рассмотрим ΔADC
По т. Пифагора
AD = √AB²-BD²
AD = √(4√3)²-(2√3)² = √48 - 12 = √36 = 6
Высота пирамиды опускается в точку пересечения биссектрис основания, поэтому HD =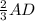 
= 4 (Т.к. биссектрисы в точке пересечения делятся 1:2 считая от вершины)
Т.к. все треугольники равносторонние ⇒ высоты у каждого треугольника пирамиды равны, то есть AD = SD
Рассмотрим ΔSHD
ΔSHD - прямоугольный, т.к. SH - высота
По т. Пифагора
SH = √SD²-HD²
SH = √6²-4² = √36-16 = √20 = 2√5
Теперь нам известны все данные для нахождения объёма пирамиды.
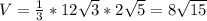
пусть 1 часть х см
тогда СЕ = 3х
DE = 4x
AE×BE=CE×DE
16 × 48 = 3x × 4x
768 = 12x^2
x^2 = 768 ÷ 12 = 64
x = 8
CE = 3x = 3 × 8 = 24
DE = 4x = 4 × 8 = 32