
Пусть дан треугольник АВС, АВ=ВС. Он тупоугольный, т.к. АС²>АВ²+ВС²
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам, и как высоты тупоугольного треугольника, проведенные к боковым сторонам, лежат вне его.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
S=h•a:2
S(ABC)=BB1•AC:2=8•15=120 см²
h=2S:a=2S(ABC):BC
AA1=CC1=240:17=240/17=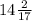 см
см

Поскольку в развёртке боковой поверхности образующая составляет с диагональю развертки угол 60⁰, а сама развертка является прямоугольником, в котором одна из сторон равна образующей (обозначим h=12см), а вторая длине окружности основания (обозначим L), то из соотношения:
tgα=L/h (отношение противолежащего катета к прилежащему), и, зная, что tg60⁰=√3, находим L:
L=h*tgα=12√3 см.
Радиус окружности основания равен:
R=L/2π=12√3/2π=6√3/π см.
S осн=πR²=π(6√3/π)²=108/π см²
V=S осн*h=108h/π=108*12/π=1296/π см³
Можно оставить так; если надо числовое значение, будет ≈412,74 см²