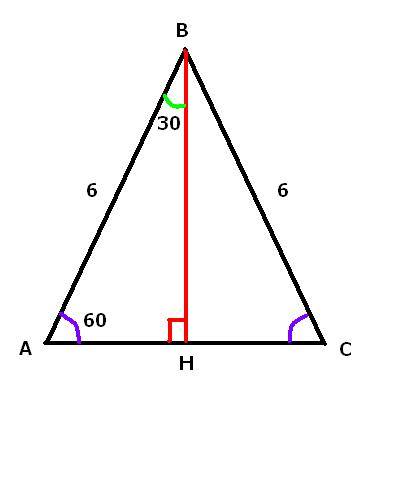
Треугольник АВС - р/б с углом при основании = 60 град. Из вершины треугольника (т.В) проведена высота ВН на основание треугольника АС. Найти высоту ВН, если боковая сторона АВ=ВС=6 см.
Т.к. АВС р/б, то высота проведенная из вершины является и биссектрисой и медианой.
Угол В= 180-60-60=60 см, значит треугольник АВС - равносторонний, тогда угол АВН=СВН=30 град. акже, если АВС - р/с, то АВ=ВС=СА=6см. Тогда, т.к. ВН - медиана, то АН=6/2=3 см. Тогда ВН по т Пиф: ВН=√(6*6-3*3)=√(36-9)=√27=√(9*3)=3√3 см
ответ: ВН=3√3 см.
Рисунок во вложении..................................... ©
Расстояние от точки до плоскости - это перпендикуляр, проведенный из этой точки к данной плоскости. Т.к. точка М равноудалена от всех сторон квадрата, то перпендикуляр из точки М будет падать в середину квадрата ( середина квадрата - пересечение его диагоналей).
Чтобы найти расстояние от точки М до сторон, нужно опустить перпендикуляр из точки М к любой из сторон квадрата.
Рассмотрим тр. ОНМ прямоугольный, (ОМ перпендикулярен плоскости квадрата, значит перпендикулярен к любой прямой, лежащей в плоскости, в данном случае ОН)
ОН=1/2 ВС=3см., ОМ=9см.
По теореме Пифагора: МН^2=ОН^2+ОМ^2
МН^2=9+81=90
МН= 3√10
По расширенной теореме синусов:
R=AB/(2sinC)=√2/(2×√2/2)=1см
ответ: 1 см
Если нужны объяснения по этой теме – обращайтесь :) Отметьте как лучший ответ, если не сложно ❤️