См. Объяснение.
Объяснение:
1) При пересечении AB и CD образуются два равных треугольника:
ΔАОС = ΔDОB, так как две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника (первый признак равенства треугольников), а именно:
АО = ОВ - согласно условию;
DO = ОС - согласно условию;
∠АОС = ∠DОB - как углы вертикальные.
2) В равных треугольниках против равных углов лежат равные стороны:
АС и BD лежат против равных углов ∠АОС и ∠DОB, следовательно:
АС=BD, - что и требовалось доказать.
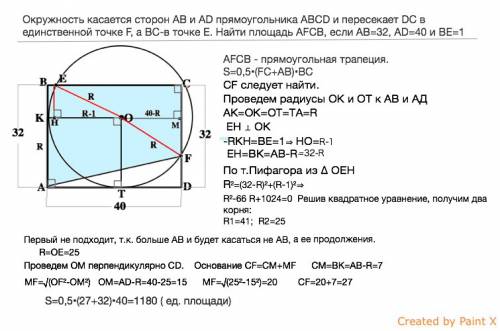
Окружность касается сторон AB и AD прямоугольника ABCD и пересекает DC в единственной точке F, а BC-в точке E.
Найти площадь AFCB, если AB=32, AD=40 и BE=1
————
АBCD- прямоугольник. ⇒
AFCB - прямоугольная трапеция. Площадь трапеции равна произведению полусуммы оснований на высоту.
S=0,5•(FC+AB)•BC
СF следует найти.
Проведем радиусы ОК и ОТ к АВ и АД соответственно.
АК=ОК=ОТ=ТА=R
Опустим из Е перпендикуляр ЕН на радиус ОК
КН=ВЕ=1⇒ НО=R-1
ЕН=ВК=АВ-R=32-R
По т.Пифагора из ∆ ОЕН
R²=(32-R)²+(R-1)²⇒
R²-66 R+1024=0 Решив квадратное уравнение, получим два корня:
R1=41; R2=25
Первый не подходит, т.к. больше, чем АВ, и будет касаться не АВ, а её продолжения.
R=ОЕ=25
Проведем ОМ перпендикулярно СD.
Основание СF=CM+MF
CM=BK=AB-R=7
MF=√(OF²-OM²)
OM=AD-R=40-25=15
MF=√(25²-15²)=20
CF=20+7=27
S=0,5•(27+32)•40=1180 ( ед. площади)
Объяснение:
х+х+38°=180°
2х=180°-38°
2х=142°
х=142°:2
х=71° <C
71°+38°=109° <A