Объяснение:
:
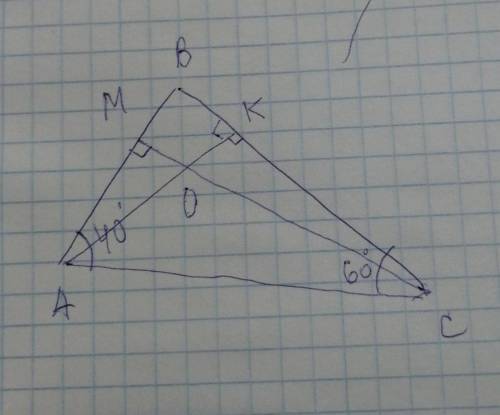
Тр-к: АВС:
<В=180-(<А+<С)=180-(40+60)=
=180-100=80 градусов
Четырехугольник МВКО:
<М=90 градусов, т. к СМ-высота
<К=90 градусов, т. к АК - высота
<В=80 градусов
<МОК=360-(<М+<В+<К)=
=360-(90+80+90)=100 градусов
<АОС=<МОК =100 градусов - как вертикальные
:
Тр-к АКС:
<АКС=90 т.,к АК - высота
<С=60 градусов
<КАС=90-<С=90-60=30 градусов
Тр-к АМС:
<АМС=90 т. к СМ- высота
<А=40 градусов
<АСМ=90-<А=90-40=50 градусов
Тр-к АОС:
<АСО=<АСМ
<ОАС=<КАС
<АОС=180-(<АСО+<ОАС) =
=180-(50+30)=180-80=100 градусов
Угол ACB пересекается параллельными прямыми⇒по теореме о пропорциональных отрезках B_1D:DC=BA_1:A_1C=1:1⇒B_1D=DC⇒AB_1=2B_1D.
Угол CAA_1 пересекается параллельными прямыми⇒по теореме о пропорциональных отрезках
AG:GA_1=AB_1:B_1D=2:1.
Таким образом, медиана BB_1 в точке пересечения разделила медиану AA_1 в отношении 2 к 1, считая от вершины. Поскольку мы взяли две произвольные медианы, доказано, что каждая из них разделит каждую в отношении 2 к 1. Поэтому во-первых они пересекаются в одной точке, а во-вторых, делятся точкой пересечения в отношении 2 к 1, считая от вершины.
Замечание для продвинутых (21+)))
Знающие теорему Чевы вопрос о том, что медианы пересекаются в одной точке, не задают. А знающие к тому же теорему Менелая, не спрашивают и про отношение 2 к 1. А знающие теорему Ван-Обеля просто умирают при этом со смеху, потому что для них решение прокручивается устно в голове за 0,5 секунды максимум