возьмём треугольник авс (ав=вс). Так как треугольник равнобедренный по условию, тогда углы при основании будут равны (180-120)/2=30 градусов.
Дальше по теореме синусов ас/sinb=bs/sina. то есть:
х/sin120=12/sin30
Тогда х=(12*sin120)/sin 30=(12*(корень из 3)/2)*2/1=12 корень из 3.
Проведём высоту вн. Так как треугольник равнобедренный, высота будет медианой и ан=нс=12 корень из 3/2=6 корень из 3.
Рассмотрим прямоугольный треугольник авн, образованный высотой вн и стороной ав, где ав=12 см по условию, а ан=6 корень из 3. По теореме Пифагора найдём длину катета вн.
аb^2=ah^2+bh^2
bh^2=ab^2-ah^2
bh^2=144-108
bh^2=36
bh=6 см
ответ: 6 см.
234
Объяснение:
Допустим дана трапеция ABCD, угол ВАС - прямой, биссектриса проведена из угла CDA, АВ=12см, CD=15см. Т.к. биссектриса делит угол пополам, то угол СDB равен углу BDA.
Угол BDA равен углу DBC как накрестлежащий. Следовательно CDB=BDA=DBC. Значит треугольник DBC - равнобедренный и сторона CD равна стороне BC, значит BC=15 см.
Проведем высоту СН к основанию AD. Т.к. трапеция прямоугольная CH=AD=12см. У нас получился прямоугольный треугольник CHD, в котором известно CH=12см, CD=15см.
Нужно найти катет HD.
Используем формулу для нахождения гипотенузы в прямоугольном треугольнике 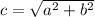
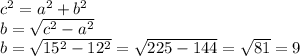
Т.к. ABCH - прямоугольник, то ВС=АH=15см. Из этого следует, что AD=15+9=24. Т.к. трапеция прямоугольная, то сторона AB - высота.
Найдем площадь трапеции по формуле 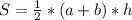
S=1/2*(15+24)*12=6*39=234
Відповідь:Переріз сфери довільною площиною є коло.
Пояснення: