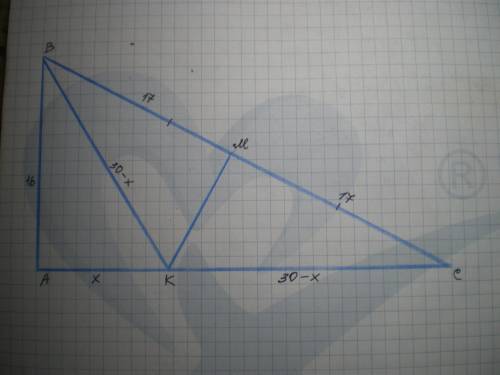
Дано: ΔАВС - прямокутний, ∠А=90°, АС=30 см, ВС=34 см; МК⊥ВС, ВМ=МС. Знайти МК.
Знайдемо АВ за теоремою Піфагора:
АВ=√(ВС²-АС²)=√(1156-900)=√256=16 см.
Проведемо ВК і розглянемо ΔВКС - рівнобедрений, тому що ВМ=СМ і МК⊥ВС, отже ВК=КС.
Нехай АК=х см, тоді КС=ВК=30-х см.
Знайдемо АК з ΔАВК - прямокутного:
АВ²=ВК²-АК²; 16² = (30-х)² - х²; 256=900-60х+х²-х²;
60х=900-256=644; х=10 11/15 см. АК=10 11/15 см, тоді
ВК = 30 - 10 11/15 = 19 4/15 = 289/15 см.
Знайдемо МК за теоремою Піфагора з ΔВМК, де ВМ=34:2=17 см.
МК²=ВК²-ВМ²=(289/15)² - 17² = (83521/225) - 289 = 18496/225.
МК=√(18496/225)=136/15=9 1\15 см.
Відповідь: 9 1/15 см.
ав= корень квадратный из ((4-0)*(4-0)+(2-4)(2-4)) = корень из 20
вс= корень кв из((2-4)(2-4) +(-2-2)*(-2-2)=корень из 20
аналогично находим что сд=да=корень из 20
теперь ас= корень из(( (2-0)*(2-0)+(-2-4)*(-2-4)= корень из 40
а вд=корень из ( (-2-4)*(-2-4) + (0-2)*(0-2)= корень из 40
в итоге если бы мы доказали что все стороны равны - то мы бы получили ромб - а доказав равенство диагоналей - подтвердили вариант с квадратом - так как у квадрата помимо равных сторон диагонали равны - в отличие от ромба.