Радіус основи і висота циліндра дорівнюють відповідно 10см і 16см Через дві точки, які лежать на колах різних основ циліндра, проведено пряму, яка знаходиться на відстані 6 см від осі циліндра. Знайдіть кут, який утворює ця пряма з віссю циліндра.
192. Диагонали параллелограмма пересекаются и точкой пересечения О делятся пополам. Треугольники АВС и АДС равновеликие (равны по площади); треугольники АОД и СОД тоже равновеликие; треугольники АОК и КОД тоже равновеликие. Следовательно, если SАДС=1/2отSАВСД, то SАОД=SСОД=1/4отSАВСД. А SКОД=1/8отSАВСД. В сумме SСОД и SКОД=3/8отSАВСД. То есть отношение 3:8.
193. Большая сторона - гипотенуза (5х). Катеты соответственно равны 4х и 3х. Треугольники, образованные высотой, прямоугольные. Все три подобны между собой. Составим пропорцию на основе подобия треугольников: ; ; . Если х=10, то гипотенуза =10*5=50, катеты: 10*4=40, 10*3=30. Периметр P=50+40+30=120.
1) Назовем треуг. АBC. Рассмотрим его. Трег. равнобедр. значит его бок.стороны по 13 см. Проведем высоту из вершины В( не из основания, а из верхнего угла треуг.) Высота по св-тву равнобедр. треуг. явл. медианой и биссек. Значит высота ВD поделит основание АС на равные части( 10:2=5). Рассмотрим треуг. АВD. BD- катет, значит найдем его по теореме Пифагора. ( 13-5 возведем в квадрат: 169-25=144. 144 это 12 в квадрате.) BD=12. А дальше просто по формуле найдем площадь. S= 1/2 a•h S= 1/2 10•12=60 ответ:60 см2.
192. Диагонали параллелограмма пересекаются и точкой пересечения О делятся пополам. Треугольники АВС и АДС равновеликие (равны по площади); треугольники АОД и СОД тоже равновеликие; треугольники АОК и КОД тоже равновеликие. Следовательно, если SАДС=1/2отSАВСД, то SАОД=SСОД=1/4отSАВСД. А SКОД=1/8отSАВСД. В сумме SСОД и SКОД=3/8отSАВСД. То есть отношение 3:8.
193. Большая сторона - гипотенуза (5х). Катеты соответственно равны 4х и 3х. Треугольники, образованные высотой, прямоугольные. Все три подобны между собой. Составим пропорцию на основе подобия треугольников: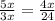
; 
; 
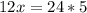. Если х=10, то гипотенуза =10*5=50, катеты: 10*4=40, 10*3=30. Периметр P=50+40+30=120.