1. Вычислите внутренний и внешний углы правильного двадцатисемиугольника.
Сумма внутренних углов многоугольника вычисляется по формуле
180(n-2), где n - количество сторон многоугольника.
180(27-2)=4500
Один внутренний угол равен 166 и 2/3 °или 166°40'
Внешний угол равен 180- 166°40'=13°20'
2. Сколько сторон имеет правильный n-угольник, если:
а)
его внутренний угол равен 170°;
180(n-2):n=170°
180 n-360=170n°
10n°=360°
n=36
б)
его внешний угол равен 12°.
Сумма внешних углом многоугольника равна 360°
n=360:12=30
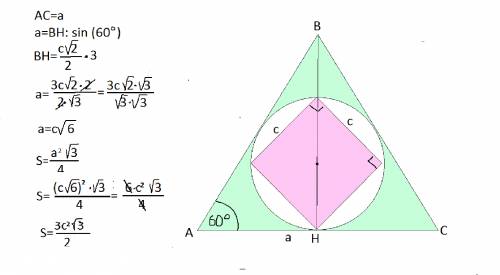
3. Около квадрата со стороной (?)см описана окружность, которая вписана в правильный треугольник. Найдите площадь треугольника.
Пусть сторона квадрата =с
Диагональ вписанного квадрата = диаметр описанной около него окружности.
Если сторона квадрата c, диаметр описанно окружности с√2
В то же время этот диаметр= 2/3 высоты описанного около этой окружности правильного треугольника.
Если 2/3=с√2, то вся высота
h=3* (с√2):2
Тогда сторона описанного правильного треугольника
а=h:sin 60°
а=3*(с√2):2}:(√3/2)=с√6
Площадь правильного треугольника
S=(a²√3):4
Подставив в эту формулу найденное значение а=с√6 стороны правильного треугольника, получим
S=(3с²√3):2
Вставив вместо с его численное значение, получим площадь конкретного треугольника.
Рисунок в дополнение к решению - во вложении.
4)
Внутри окружности с радиусом 8 см расположены две окружности, касающиеся друг друга внешним образом, каждая из которых касается большей окружности внутренним образом, причем все точки касания и радиусы всех трех окружностей лежат на одной прямой.
К задаче с таким условием можно сделать рисунок - и только.
1. Вычислите внутренний и внешний углы правильного двадцатисемиугольника.
Сумма внутренних углов многоугольника вычисляется по формуле
180(n-2), где n - количество сторон многоугольника.
180(27-2)=4500
Один внутренний угол равен 166 и 2/3 °или 166°40'
Внешний угол равен 180- 166°40'=13°20'
2. Сколько сторон имеет правильный n-угольник, если:
а)
его внутренний угол равен 170°;
180(n-2):n=170°
180 n-360=170n°
10n°=360°
n=36
б)
его внешний угол равен 12°.
Сумма внешних углом многоугольника равна 360°
n=360:12=30
3. Около квадрата со стороной (?)см описана окружность, которая вписана в правильный треугольник. Найдите площадь треугольника.
Пусть сторона квадрата =с
Диагональ вписанного квадрата = диаметр описанной около него окружности.
Если сторона квадрата c, диаметр описанно окружности с√2
В то же время этот диаметр= 2/3 высоты описанного около этой окружности правильного треугольника.
Если 2/3=с√2, то вся высота
h=3* (с√2):2
Тогда сторона описанного правильного треугольника
а=h:sin 60°
а=3*(с√2):2}:(√3/2)=с√6
Площадь правильного треугольника
S=(a²√3):4
Подставив в эту формулу найденное значение а=с√6 стороны правильного треугольника, получим
S=(3с²√3):2
Вставив вместо с его численное значение, получим площадь конкретного треугольника.
Рисунок в дополнение к решению - во вложении.
4)
Внутри окружности с радиусом 8 см расположены две окружности, касающиеся друг друга внешним образом, каждая из которых касается большей окружности внутренним образом, причем все точки касания и радиусы всех трех окружностей лежат на одной прямой.
К задаче с таким условием можно сделать рисунок - и только.

Чертёж смотрите во вложении.
Дано:
ΔАВС.
ВО - биссектриса ∠АВС.
АК - биссектриса ∠ВАС.
Точка М - точка пересечения ВО и АК.
∠АМВ = 177°.
Найти:
∠ВСА = ?
Пусть ∠АВМ = х, тогда и ∠МВК = х (так как ВО - биссектриса ∠АВС) ; ∠ВАМ = ∠МАО = у (так как АК - биссектриса ∠ВАС).
Рассмотрим ΔАМВ. ∠ВМК - внешний, и так как он с ∠АМВ смежный, то ∠ВМК = 180°-177° = 3°. Так как ∠ВМК - внешний, то он равен сумме углов не смежных с ним. То есть, х+y = 3°.
∠АВС = x+x = 2x
∠ВАС = у+у = 2у.
х+у = 3°
2*(х+у) = 2*3°
2х+2у = 6°.
Тогда, по теореме о сумме углов треугольника -
∠ВСА = 180°-(2х+2у)
∠ВСА = 180°-6°
∠ВСА = 174°.
ответ: 174°.