Відповідь : 
Пояснення:
рівняння прямої через дві точки:

-8(х-6)= -24(у-1); / : -8
х-6=3у-3;
3у=x-6+3;

6. Дано: ΔАВС, СР-биссектриса, АР=4 см, ВР=5 см
Найти: Периметр ΔАВС
1. СР- биссектриса ΔАВС => АР:ВР=АС:ВС
4:5=10:ВС
ВС=(5*10):4=12,5 (см)
2. Р(АВС)=АВ+ВС+АС=(АР+ВР)+ВС+АС
Р(АВС)=4+5+12,5+10= 31,5 (см)
ответ: 31,5 см
Объяснение:
7. Позначимо ромба АВСD, АВ = 5см, О - точка перетину діагоналей АС і ВD, АС = 6см. Знайти висоту АК
Розв"язання:
Діагоналі ромба рівні, звідси, АО = СО = АС/2=6/2=3, ВО = ОD
З прямокутного трикутника АВО( кут АОВ = 90 градусів):
За т. Піфагора
Звідси, діагональ ВD = 2ВО = 2*4= 8см.
Знаходимо полщу ромба
Тоді висота ромба дорівнює:
Відповідь: 4.8 см.
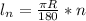 , где n - градусная мера соответственного центрального угла.
, где n - градусная мера соответственного центрального угла.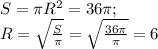 , где S - площадь круга.
, где S - площадь круга.
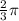 см.
см.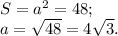
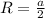 , где a - сторона квадрата.
, где a - сторона квадрата.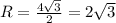
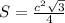 , где c - сторона правильного треугольника.
, где c - сторона правильного треугольника.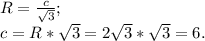
 .
.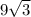 см.
см.
у=1/3х-1
Объяснение:
оскільки дані точки мають різні абсциси ,то пряма СD є вертикальною ,Тоді можна скористатися рівнянням прямої у вигляді : у=kx+b.
підставивши координати точок С і D у рівняння отримаємо:
6k+p=1
-18+p=-7
k=1/3
p=-1
звідси рівняння прямої: у=1/3х-1