Объяснение:
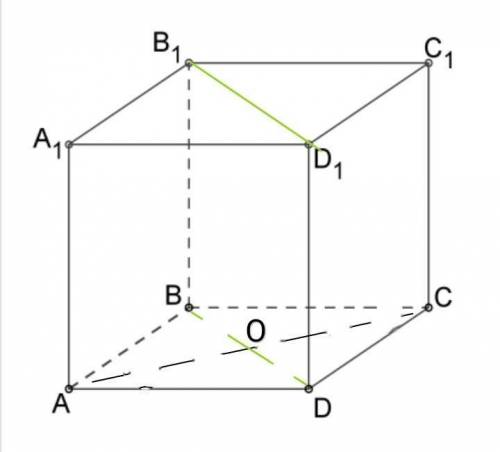
1) Все грани куба являются квадратами.
По свойствам квадрата диагонали взаимно перпендикулярны. В нашем случае АС ⟂ BD.
2) DD1 ⟂ DC по условию и DD1 ⟂ DA, DC ⋂ DA = D, тогда по признаку перпендикулярности прямой и плоскости DD1 ⟂ (ABC).
3) Так как DD1 ⟂ (ABC) , то она перпендикулярна любой прямой, лежащей в этой плоскости, в том числе DD1 ⟂ AC.
4) Получили, что
АС ⟂ BD, AC ⟂ DD1, BD ⋂ DD1 = D, тогда по признаку перпендикулярности прямой и плоскости АС ⟂ (ВВ1D1), что и требовалось доказать.
Розв'язок:
де a — одна із сторін трикутника, hₐ — висота, опущена на сторону a.
Виразимо із формули hₐ і підставимо значення:
Відповідь: висота трикутника рівна 5 см.