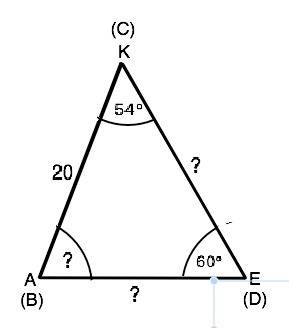
Для начала найдем неизвестные угол и стороны ∆ АКЕ. Сумма углов треугольника 180° => угол КАЕ=180°-(54°+60°=66°
По т.синусов АЕ=АК•sin54°/sin60°. KE=AK•sin66°/sin60°
sin60°=0.8660; sin54°= 0.8090; sin66°=0.9135
AE=20•0,8090/0,8660=18,683≈18,7 см; KE=20•0,9135/0,8660=21,097≈ 21,1 см
Стороны и углы треугольника ВСD имеют те же значения, что и соответствующие углы и стороны ∆ АКЕ, но в условии не указано, какие именно элементы двух треугольников равны. Если в ∆ ВСD сторона ВС=АК, и ∠D=∠Е, то ∠В=∠А=66°,∠С=∠К=54°, ВС=20 см, ВD=AE≈18,7= см, CD=KE≈21,1 см
1. равнобедренный треугольник это треугольник у которого 2 стороны равны.
2Теорема о свойствах равнобедренного треугольника. В любом равнобедренном треугольнике: 1) углы при основании равны; 2) медиана, биссектриса и высота, проведенные к основанию, совпадают. Доказательство. Оба эти свойства доказываются совершенно одинаково. Рассмотрим равнобедренный треугольник АВС, в котором АВ = ВС. Пусть ВВ1 - биссектриса этого треугольника. Как известно, прямая BB1 является ось симметрии угла АВС. но в силу равенства AB = BC при той симметрии точка А переходит в С. Следовательно, треугольники ABB1 и CBB1 равны. Отсюда все и следует. Ведь в равных фигурах равны все соответствующие элементы. Значит, ÐBAB1 = ÐBCB1. Пункт 1) доказан. Кроме этого, AB1 = CB1, т. е. BB1 - медиана и ÐBB1A = ÐBB1C = 90°; таким образом, BB1 также и высота треугольника ABC.
3АС=АВ+ВС=34+12=46 либо же
АС=АВ-ВС= 34-12=22