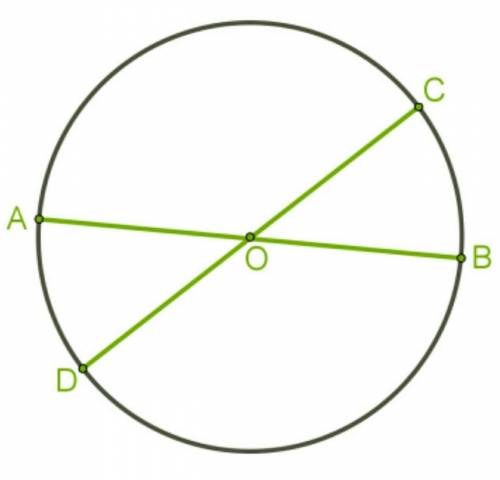
68. По данным на рисунке найдите площадь 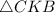 .
.
ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :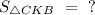 Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.
Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно, 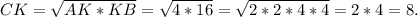
Следовательно, 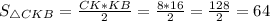 ед².
ед².
64 ед².
- - -70. ABCD - прямоугольник. Найдите 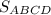 .
.
Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :
Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно, 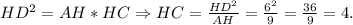
Следовательно, 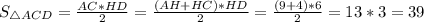 ед².
ед².
Тогда 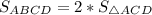 = 2*39 ед² = 78 ед².
= 2*39 ед² = 78 ед².
78 ед².
а=24/4=6 см, боковое ребро ⊥ основанию и равно 10,
площадь полной поверхности призмы равна Sбок+2Sосн, Sбок = 10*4а=
10*24=240 см², Sосн= а²= 6²=36 см², Sполн=Sбок+2Sосн=240+2*36=
240+72=312 см²,
основание правильной треугольной призмы- равносторонний Δ со стороной а=24/3=8 см, и тремя равными углами α= 180°/3=60°,
Sосн= а²sin60°/2= (8²*√3/2)/2=64√3/4= 16√3 см²,
боковое ребро ⊥ основанию и равно 10 см, т е
Sбок= 3а*h= 3*8*10=240 см², Sполн= Sбок+2Sосн= 240+ 32√3,
сравним площади полных поверхностей этих призм:
312=240+72 > 240+32√3, (√3 < 2) , т е у нас полная поверхность
четырехугольной призмы больше треугольной