Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы.
По т.Пифагора с²=a²+b², где с - гипотенуза, a и b – катеты.
с=√(9²+12²)=15
R=15:2=7,5 см
Подробно.
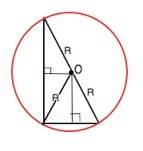
Центр описанной окружности треугольника лежит на пересечении срединных перпендикуляров к его сторонам.
Срединные перпендикуляры прямоугольного треугольника пересекаются на середине гипотенузы, следовательно центр описанной окружности - середина гипотенузы, и радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. R=7,5 см.
Пусть дан прямоугольник ABCD (AB=CD, BC=AD), AB=CD = 5м (по условию), АС = 13м (по условию).
Рассмотрим ΔABC (∠B=90°) => BC^2 = AC^2 - AB^2
BC^2 = 169 - 25
BC^2 = 144
BC = 12
S прямоугольника равна:=S = ab => S= 12*5 = 60 (м^2)