Объяснение:
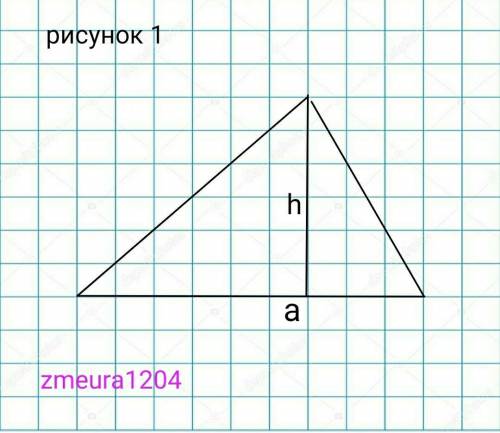
1) рисунок 1.
Дано:
Треугольник
а=48см
S=72cм²
h=?
Решение
S=1/2*a*h, где а- сторона треугольника, h- высота опущенная на сторону а.
h=2*S/a=2*72/48=3 см
ответ: 3см.
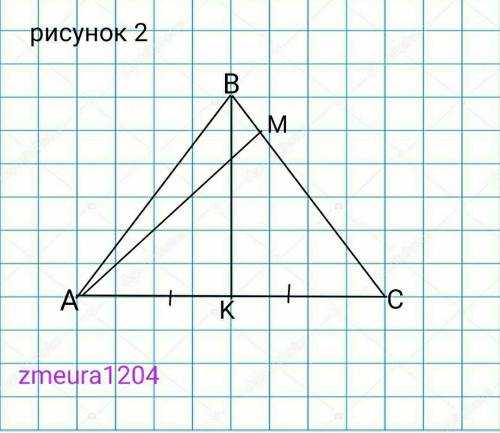
2) рисунок 2
Дано
∆АВС- равнобедренный
АВ=ВС
АС=20см
ВК=24см
АС=?
Решение
ВК- высота, медиана и биссектрисса, равнобедренного треугольника ∆АВС.
АК=КС
КС=АС:2=20:2=10см.
∆ВКС- прямоугольный треугольник.
По теореме Пифагора
ВС=√(ВК²+КС²)=√(24²+10²)=26см.
S=1/2*BK*AC=1/2*24*20=240 см²
S=1/2*AM*BC
AM=2*S/BC=2*240/26=480/26=
=18цел6/13 см
ответ: АМ=18цел6/13 см
Сделаем рисунок и обозначим вершины пирамиды АВСА1В1С1. Ребро ВВ1⊥АВС=1 см
Площадь боковой поверхности этой пирамиды - сумма площадей трех трапеций: двух прямоугольных и одной равнобедренной - той, что противолежит ребру ВВ1.
В основаниях пирамиды правильные треугольники - следовательно, длины средней линии всех трапеций равны 0,5•(3+5)=4 см
Площадь прямоугольных граней равна произведению их средней линии на длину высоты пирамиды, т.е. .
S (АВВ1А1)=S (ВВ1С1С)= 4•1=4 см²
Чтобы найти высоту грани АА1С1С, проведем в основаниях пирамиды высоты ВН и В1К и соединим К и Н.
Плоскость прямоугольной трапеции ВНКВ1 перпендикулярна плоскости оснований, т.к. содержит в себе отрезок ВВ1, перпендикулярный обоим основаниям.
Из К опустим высоту КТ.
КН по теореме о трех перпендикулярах перпендикулярна АС и является высотой трапеции АСС1А1.
В прямоугольном треугольнике КТН катет КТ=ВВ1=1см, катет НТ равен разности высот оснований пирамиды.
ВК=(3√3):2
BH=(5√3):2
ТН=2√3):2=√3 см
КН=√(КТ²+НТ²)=√4=2 см
S (АСС1А1)=4*2=8 см²
S(бок)=4+4+8=16 см²

Найдите по теореме Пифагора половину основания треугольника, которое составляет грань пирамиды. Затем площадь этой грани, и ее уже умножить следует на 3. Это будет площадь боковой поверхности пирамиды.
Объяснение: