Геометрия: по геометрии 5 и 4 номера по геометрии 5 и 4 номера. >

по геометрии 5 и 4 номера по геометрии 5 и 4 номера. ">

👇

Увидеть ответ

Ответ:

nastosetrova1

22.01.2021

4. Средняя линия MN равна половине AC.

С теоремы Пифагора ищем AC:

AC = √(√136)² - 10² = √136 - 100 = √36 = 6

MN = 6 : 2 = 3

ответ: 3

5. Верные суждения под номерами 2 и 3.

4,5(92 оценок)

Открыть все ответы

Ответ:

БлинчикТян

22.01.2021

Случай 1 : Площадь бо́льшего треугольника равна 8 (ед²).Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.

Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.

Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).

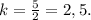
$k = \frac{5}{2} = 2,5.$

Площади подобных треугольников относятся как квадрат коэффициента подобия.

Отсюда -

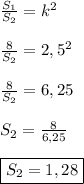
$\frac{S_{1} }{S_{2} } = k^{2} \\\\\frac{8}{S_{2} } = 2,5^{2} \\\\\frac{8}{S_{2} } = 6,25\\\\S_{2} = \frac{8}{6,25} \\\\\boxed{S_{2} = 1,28}$

1,28 (ед²).

- - -

Случай 2 - Площадь меньшего треугольника равна 8 (ед²).

В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).

S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника

Тогда -

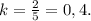
$k = \frac{2}{5} = 0,4.$

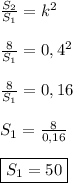
$\frac{S_{2} }{S_{1} } = k^{2}\\\\\frac{8 }{S_{1} } = 0,4^{2}\\\\\frac{8 }{S_{1} } = 0,16\\\\S_{1} = \frac{8}{0,16}\\\\\boxed{S_{1} = 50}$

50 (ед²).

4,8(24 оценок)

Ответ:

MATVEYPRO26

22.01.2021

Длина двух сторон равнобедренного треугольника составляет 5 см и 7 см. Какой может быть периметр этого треугольника?

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Решение :Равнобедренный треугольник - это такой треугольник, две стороны которого равны между собой.

Для выполнения задания также необходимо учесть и неравенство треугольника (каждая сторона треугольника меньше суммы двух других сторон).

Допустим, что основание равно 5 см, тогда боковые стороны равны по 7 см.

"Проверяем" каждую сторону -

7 см + 7 см > 5 см - верное неравенство.

7 см + 5 см > 7 см - верное неравенство.

Как видим, все неравенства верны, следовательно, такой треугольник существует. Тогда его периметр (сумма длин всех сторон) равен 5 см + 7 см + 7 см = 19 см.

Теперь допустим, что основание равно 7 см, тогда боковые стороны равны по 5 см.

Аналогично -

5 см + 5 см > 7 см - верное неравенство.

7 см + 5 см > 5 см - верное неравенство.

Неравенства верны, треугольник существует. Тогда его периметр равен 5 см + 5 см + 7 см = 17 см.

ответ : 19 см и 17 см.

4,4(58 оценок)

Это интересно:

Компьютеры-и-электроника

20.04.2021

Как увеличить размер ластика в MS Paint на ноутбуках с Windows 7...

Дом-и-сад