Трикутники авс і а1в1с1 подібні , ав= 7см, вс = 6см, ас= 5см. знайти периметр трикутника, якщо В1С1= 2см.

👇

Увидеть ответ

Ответ:

inessa30

14.06.2020

Відповідь: 6 см

Пояснення:

за першою ознакою подібності трикутників віднайдемо А₁В₁ та А₁С₁:

А₁В₁ : АВ= С : ВС;

А₁В₁= (АВ*В₁С₁) :ВС= 7*2/6=7/3( см)

А₁С₁: АС = В₁С₁ : ВС;

А₁С₁= (АС*В₁С₁) :ВС= 5*2/6=5/3 см

Знайдемо периметр трикутника А₁В₁С₁

Р=2+7/3+5/3=2+12/3=6 см

ІІ варіант так як всі сторони подібні, то і периметри будуть подібні

Р(АВС)=7+6+5=18см

Р(АВС):Р(А₁В₁С₁)= ВС : В₁С₁;

Р(А₁В₁С₁)=Р(АВС)*В₁С₁/ВС=18*2/6=6 см

4,4(5 оценок)

Открыть все ответы

Ответ:

MaxKryaks

14.06.2020

Точка О2 - центр вписанной окружности в тр-ник АВС. Точка О1 - центр заданной окружности.
Около тр-ка АВС опишем окружность.
АО2, ВО2 и СО2 - биссектрисы соответствующих углов.
Продолжим отрезок СО2 до пересечения его с описанной окружностью в некой точке К.
∠АО2К=∠А/2+∠С/2, т.к. ∠АО2К является внешним к тр-ку АСО2.
∠ВАК=АВК=∠С/2, т.к. оба опираются на те же дуги, на которые опираются равные углы из вершины тр-ка АВС. КА=КВ по этой же причине.
Заметим, что в тр-ке АКО2 ∠КАО2=∠АО2К, значит он равнобедренный.
КА=КО2=КВ, значит точка К - центр описанной около тр-ка АВО2 окружности.
Тр-ник АВС - равнобедренный. В нём СМ - биссектриса и высота. В прямоугольном тр-ке АСМ ∠А+∠С=90°. Заметим, что и в тр-ке АСК ∠САК=90°, значит ∠CВК=90°. СА и CВ - касательные к окружности с центром в точке К. Точки А и В лежат на этой окружности. Но СА и CВ - касательные к заданной окружности, значит точки К и О1 совпадают.
О1О2 - радиус заданной окружности, значит центр вписанной в тр-ник АВС окружности лежит на данной окружности.
Доказано.
Две прямые, касающиеся данной окружности в точках а и в, пересекаются в точке с. докажите, что центр

Две прямые, касающиеся данной окружности в точках а и в, пересекаются в точке с. докажите, что центр

4,7(62 оценок)

Ответ:

darkforse876

14.06.2020

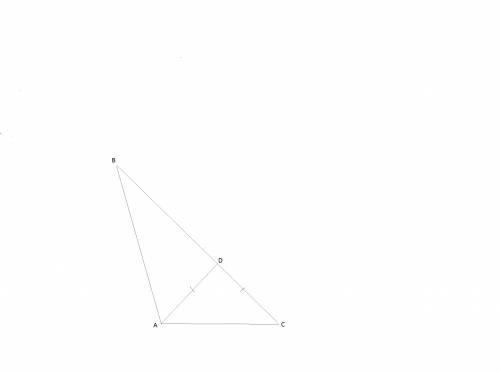
Внутри треугольника ABC к стороне BC проведена прямая AD так, что получился равнобедренный треугольник ADC с основанием AC.
Найдите длину основания AC, если периметры треугольников ABC и ABD

равны соответственно 39 см и 27 см

Решение

Рассмотрим оба треугольника.

Если из треугольника АВС вырезать АС, то, так как АD=DС, получим периметр треугольника АВD.
Р АВС - Р АВD= АС
АС=39-27=12 см

Если трубуется, есть и второй вариант решения:

Запишем периметры обоих треугольниокв в виде суммы их сторон

Р ᐃ АВС=АВ+ВС+АС=39 см

а так ВС=ВD+DС, то

Р ᐃ АВС=АВ+ВD+DС+АС=39 см

Периметр ᐃ АВD=АВ+ВD+АD=27 см

Так как АD=DС, то можем записать

Р ᐃ АВD=АВ+ВD +DС =27 см

Составим систему: