Question

10клас Визначте чи лежать точки А,В і С на одній прямій, якщо А(0;0;-1) , В(0;0;8) С (0;0;11). Відповідь обґрунтуйте.

Answer 1

Точки А, В і С лежать на одній прямій.

Объяснение:

Знайдемо ненульовий елемент першого вектора:

AB$АВ_{z}$=9

n = $\frac{AC_{Z} }{AB_{Z} }$=$\frac{12}{9}$=$\frac{4}{3}$

$\frac{4}{3}$ * AB = ($\frac{4}{3}$ * AB$_{X}$; $\frac{4}{3}$ * ABy; $\frac{4}{3}$ * ABz} = ( $\frac{4}{3}$ * 0;  $\frac{4}{3}$ * 0; $\frac{4}{3}$ * 9) = (0; 0; 12)

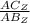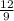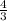
Відповідь: Оскільки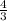 $\frac{4}{3}$AB = AC, то вектора колінеарні, і, отже, точки А, В і С лежать на одній прямій.