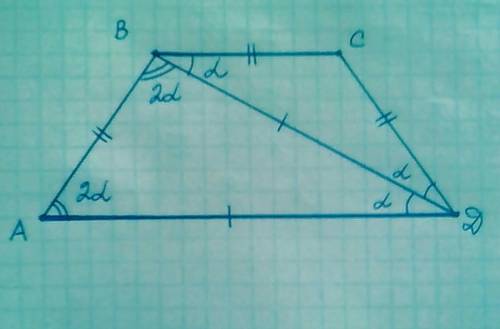
1) Рассмотрим ∆ ВСD:
Пусть угол CBD = a , тогда угол BDC = a, так как ∆ ВСD - равнобедренный
угол СBD = угол АDB = a - как накрест лежащие углы при ВС || АD и секущей BD
По свойству равнобедренной трапеции:
Углы при основании равнобедренной трапеции равны
Значит, угол BAD = угол ADC = 2a
2) Рассмотрим ∆ ABD:
∆ ABD - равнобедренный , поэтому угол BAD = угол АВD = 2a
Сумма всех углов в любом треугольнике всегда равна 180° =>
угол ВАD + угол ABD + угол ADB = 180°
2a + 2a + a = 180°
5a = 180°
a = 180° : 5 = 36°
Угол при меньшем основании ( ВС ) равнобедренной трапеции равен:
угол ABC = 3a = 3 × 36 = 108°
ОТВЕТ: 108°
Диагональ делит параллелограмм на 2 равных треугольника. Считаем площадь одного, умножаем на 2 и - вуаля! (площадь треугольника считаем по формуле S = a*b*sin(C)/2). Окончательно
S = 14*8,1*(1/2) = 56,7.
Ну хорошо, поступила без синусов. Тогда так. Из вершины диагонали, которая НЕ общая с заданной стороной, опускаем перпендикуляр на эту сторону. Это - высота параллелограмма (и того треугольника, про который я говорил - тоже, но это не важно). У нас получился прямоугольный треугольник, у которого острый угол 30 градусов, а высота - противолежащий катет (углу в 30 градусов). Поэтому высота равна половине гипотенузы этого треугольника, то есть - в данном случае - диагонали параллелограмма. То есть высота параллелограмма равна 14/2 = 7.
S = 7*8,1 = ... ну, вы уже в курсе :