Ребра тетраэдра по условию равны, следовательно, он правильный и все его грани - правильные треугольники.
Каждая сторона сечения соединяет середины сторон такого треугольника и, как средняя линия соответствующей грани, равна половине параллельного ей ребра.
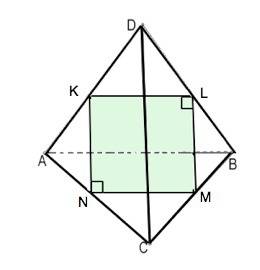
Скрещивающиеся ребра правильного тетраэдра перпендикулярны. DC⊥АВ⇒СD⊥MN, т.к. MN||АВ.
КN||CD⇒ KN⊥MN. Аналогично доказывается перпендикулярность всех соседних сторон сечения KLMN . Следовательно сечение- квадрат со стороной 38:2=19.
Площадь сечения 19²=361 (ед. площади)
ответ:∠АВС=20°
Объяснение:
Рассмотрим Δ АДС.
В этом треугольнике углы.
60°; х°; х/2 °. (биссектриса делит угол С пополам)
60+х+х/2=180.
1,5х=120.
х=80°(угол А)
х/2=80/2=40° (∠ВСД).
Найдем угол ВДС.
Этот угол смежный с углом АДС.
180-60=120°
Рассмотрим Δ ДВС.
Найдем ∠ В.
180-120-40=20°.