1), 2), 6), 8).
Объяснение:
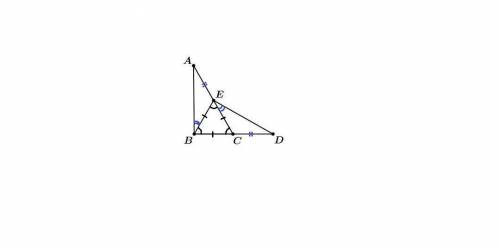
ΔАВС = ΔDEB,
АВ = DE, АС = DB, значит ВС = ВЕ, т.е. ΔВЕС равнобедренный
В равных треугольниках против равных сторон лежат равные углы, значит
∠DBE = ∠ACB, тогда
ΔВЕС равнобедренный с основанием ВС.
Итак, ВЕ = ЕС = ВС, т.е. ΔВЕС равносторонний.
∠АВЕ = ∠АВС - ∠ЕВС
∠DEC = ∠DEB - ∠BEC
∠АВС = ∠DEB из равенства треугольников,
∠EBC = ∠BEC, как углы равностороннего треугольника, значит
∠АВЕ = ∠DEC.
АЕ = АС - ЕС
CD = DB - BC
AC = DB по условию,
ЕС = ВС, так как ΔВЕС равносторонний, значит
АЕ = CD.
1) Треугольник BCE равнобедренный - верно.
2) Треугольник BCE равносторонний - верно.
3) ∠ABC = 90° - нельзя утверждать.
4) Треугольник ECD равнобедренный - нельзя утверждать.
5) AE = BC - нельзя утверждать.
6) AE = CD - верно.
7) ∠ABE = ∠CDE - нельзя утверждать.
8) ∠ABE = ∠CED - верно.
ответ:S=16π
Объяснение:в основании образуется треугольник, состоящий из двух радиусов, к-ые относятся к дуге с 60°, и сторонной, полученной сечением квадрата. Сторону квадрата находим по Пифагору: √(a²+a²) = 4√2, a = 4. Основание треугольника так же равно 4. Этот треугольник, в первую очередь, является равнобедренным, так как имеет две равных сторон (радиусов окружности), но по той причине, что вершина равна 60, это правильный треугольник. Следовательно, все его стороны равны, что указывает, что радиусы равны 4. Зная радиус, мы можем найти длину окружности: 2πr=4π. Высотой цилиндра является сторона квадрата, т.к. второй пересекает его параллельно оси. Отсюда S=4π*4=16π
ответ: 81+84 =165величина угла пересекаются водной точке
Объяснение: