Правильная четырёхугольная пирамида 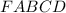 .
.
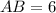 (см).
(см).
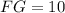 (см).
(см).
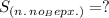 (см²).
(см²).
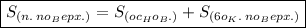
Значит сначала мы должны найти площадь основания пирамиды, а затем площадь боковой поверхности пирамиды.
В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому 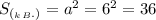 (см²).
(см²).
Значит нам нужно сначала найти апофему нашей пирамиды.
1 правило: Апофема делит сторону основания пополам.2 правило: Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды.Объяснение 1 правила: из этого следует, что апофема  делит сторону основания
делит сторону основания  так, что
так, что 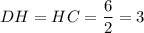 (см).
(см).
Объяснение 2 правила: внутри нашей пирамиды образовался прямоугольный 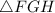 , где
, где 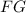 - катет прямоугольного тр-ка (высота пирамиды);
- катет прямоугольного тр-ка (высота пирамиды); 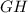 - катет прямоугольного тр-ка;
- катет прямоугольного тр-ка; 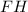 - гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что
- гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что 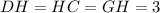 (см).
(см).
Так как апофема 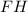 нашей пирамиды является ещё и гипотенузы прямоугольного
нашей пирамиды является ещё и гипотенузы прямоугольного  , то мы сможем найти её величину по т.Пифагора:
, то мы сможем найти её величину по т.Пифагора:
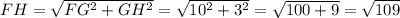 (см).
(см).
Теперь найдём периметр основания (квадрата):
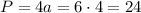 (см).
(см).
Затем найдём площадь боковой поверхности:
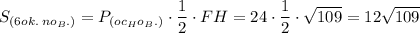 (см²).
(см²).
Остаётся найти ответ на вопрос: "Чему равна площадь полной поверхности пирамиды?"
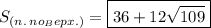 (см²).
(см²).
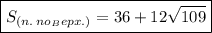 (см²).
(см²). 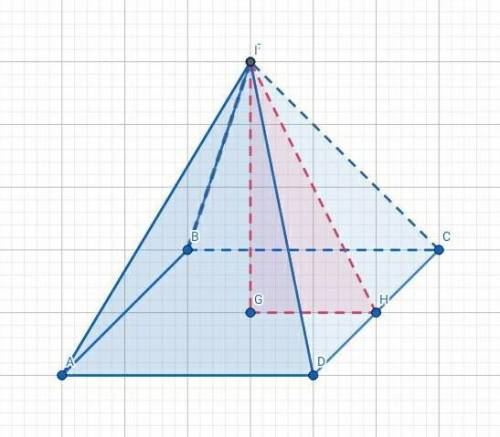
Ребро DС тетраэдра DABC перпендикулярно плоскости АВС. Известно, что АВ=5 см, АС =7 см, ВС=DC= 4 Корня из 2 см. Найдите угол между прямыми BD и Ас.
1
СМОТРЕТЬ ОТВЕТ
Войди чтобы добавить комментарий
ответ
0
alinaromanova84
середнячок
5 ответов
10 пользователей, получивших
Дано: ABCD - тетраэдр;
Определим линейную меру двугранного угла DACB.
ADC ⊥ пл. АВС, тогда двугранный угол DACB и соответствующий ему линейный угол DCB равны 90о.
Определим линейную меру двугранного угла DABC.
Проведем отрезок СМ ⊥ АВ, соединим точки М и D.
то по теореме о 3-х перпендикулярах,
По определению, ∠DMC - линейный угол двугранного угла DABC.
По теореме Пифагора:
Тогда
Отсюда
Определим линейную меру двугранного угла BDCA.
то ∠АВС - линейный угол двугранного угла
ответ:90°,45°,60°
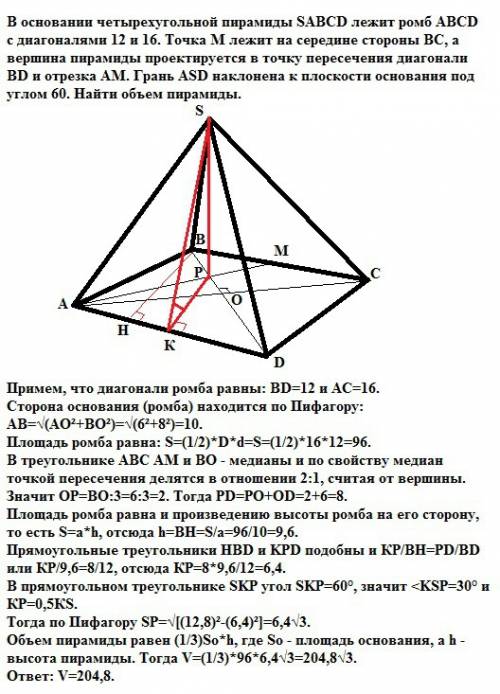
12(3+√109) см²
Объяснение:
Высота пирамиды проецируется в центр вписанной окружности ( с радиусом r), поскольку расстояние от вершины пирамиды до сторон основания равны
S осн = 6*6=36 см²
S б = 1/2*Ро*k, Ро=6*4=24 см
S б =1/2*24*√109=12√109 см²
r= 6/2=3 ( в квадрате радиус впис. окружности равен половины стороны квадрата)
k=√109=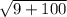 - апофема ( расстояние от вершины пирамиды до стороны основания)
- апофема ( расстояние от вершины пирамиды до стороны основания)
S полное = 36 +12√109=12(3+√109) см²