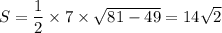а) Припустимо, що кути при більшій основі мають 3х° та 2х°, тоді кути при меншій основі мають 6х° та 4х°. Очевидно, що вони не можуть бути розташовані у послідовному порядку. Крім того, такої трапеції взагалі не існує, тому що сума кутів, прилеглих до бічної сторони трапеції, повинна становити 180°. В даному випадку ця умова не витримується.
б) ∠А:∠В:∠С:∠D=8:7:13:12, тобто, виконується умова задачі, при цьому ∠А+∠D=180° і ∠В+∠С=180°. Відповідь: такі кути можуть бути розташовані у послідовному порядку.
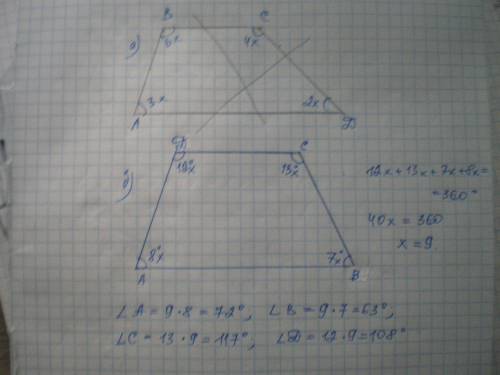
Поскольку плоскость сечения параллельна оси цилиндра, сечением будет прямоугольник с высотой H, равной высоте цилиндра, и основанием длиной L, являющемся хордой, лежащей в основании цилиндра. Также известно, что диагональ прямоугольника имеет наклон в 60 градусов к его основанию. Отсюда можно записать следующие соотношения:
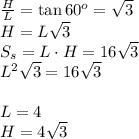
Далее проведем отрезки, соединяющие концы хорды с центром основания цилиндра. Получится равнобедренный треугольник с углом в вершине 120 градусов и бедрами, равными радиусу основания цилиндра. Проведя в этом треугольнике высоту из вешины к хорде, получим два прямоугольных треугольника, одним из катетов которых является половина хорды. Поскольку угол между этими катетами и гипотенузой равен 30 градусам, можно записать следующее соотношение между длиной хорды и радиусом основания цилиндра:
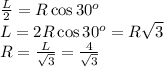
Запишем теперь выражение для площади боковой поверхности цилиндра:
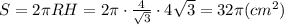
ответ: Площадь боковой поверхности цилиндра равна 32пи кв. см
(см. объяснение)
Объяснение:
1-ый случай:
AB и BC - катеты.
Тогда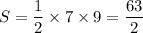 .
.
2-ой случай:
AB - катет, BC - гипотенуза.
Тогда