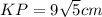1. Обозначим точки пересечения с прямой L: А1 и В1 соответственно точкам А и В. Расстояние от точки до прямой определяется длиной перпендикуляра, следовательно, надо найти АА1. Когда сделаем чертеж, получим прямоугольную трапецию АА1ВВ1. Обозначим точку на прямой l M1. То есть: АА1, BB1 и MM1 ⊥ L, и AA1, MM1 и ВВ1 ║L.
2. Зная, что АМ=МВ (по условию) и АА1, ММ1 и ВВ1 ║а (п. 1) получим: А1М1=М1В1 (по теореме Фалеса).
3. Найдем АА1 по формуле средней линии трапеции: (АА1+12)/2=16, отсюда АА1 = 20 см.
ответ: 20 см
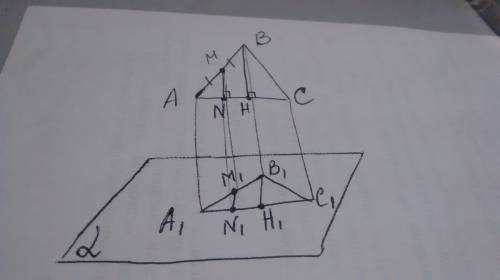
При пересечении диагонали ромба точкой пересечения деляться пополам. Также диагонали перепендикулярны друг другу. Получается 4 прямоугольных треугольника. Если угол NPK = 60°, то угол PKM = 30°, по свойству прямоугольного треугольника. Катет OP (О - точка пересечения диагоналей) равен половине отрезка OK потому, что лежит напротив угла в 30°. OK = MK : 2 = 18см значит OP = 18 : 2 = 9см.
Находим гипотенузу треугольника, т.е. сторону ромба по теореме Пифагора:
ОТВЕТ: