Question

Даны вершины треугольника АВС: А (0;4), В (-2;4), С (-1;3). Найдите угол А в треугольнике АВС.

Answer 1

Объяснение: два решения, так как не знаю какую тему проходите.

1. решение.

Найдем длины сторон.

АВ =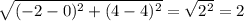$\sqrt{(-2-0)^2+(4-4)^2} = \sqrt{2^2} = 2$

AC =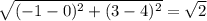 $\sqrt{(-1-0)^2+(3-4)^2} = \sqrt{2}$

BC =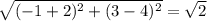 $\sqrt{(-1+2)^2+(3-4)^2}=\sqrt{2}$

По теореме косинусов

BC²=AB²+AC²-2AC*AB*cosA и отсюда

cosA =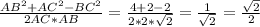 $\frac{AB^2+AC^2-BC^2}{2AC*AB} = \frac{4+2-2}{2*2*\sqrt{2} } = \frac{1}{\sqrt{2}} = \frac{\sqrt{2} }{2}$

Угол А = 45°

2 решение

Найдем координаты векторов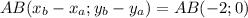 $AB(x_b-x_a;y_b-y_a) = AB(-2;0)$

Аналогично АС(-1;-1)

Найдем модули векторов

|AB| =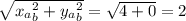 $\sqrt{x_a_b^2+y_a_b^2} = \sqrt{4+0} = 2$

Аналогично |AC| =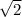 $\sqrt{2}$  кстати, модуль вектора и есть его длина и мы эти длины уже рассчитали выше.

Скалярным произведением двух векторов является сумма произведений соответствующих координат этих векторов.

(AB*AC) = (-2*(-1)) + 0*(-1)) = 2

Тогда из формулы скалярного произведения векторов АВ и АС

cosA =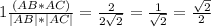 $1\frac{(AB*AC)}{|AB|*|AC|} = \frac{2}{2\sqrt{2} } = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$

cosA = 45°