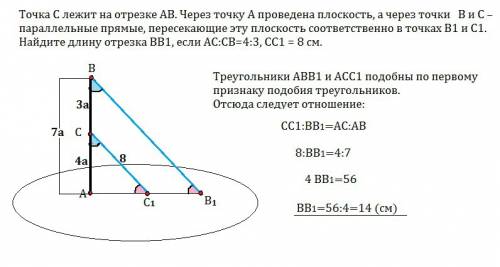
Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С – параллельные прямые, пересекающие эту плоскость соответственно в точках В1 и С1.
Найдите длину отрезка ВВ1, если АС:СВ=4:3, СС1 = 8 см.
––––––––––
Через две параллельные прямые можно провести плоскость, притом только одну. ⇒
ВВ1 и СС1 лежат в одной плоскости.
Точки А, В, С. принадлежат отрезку АВ. ⇒ АВ ∈ той же плоскости.
Плоскость, проведенная через А, и плоскость, содержащая СС1 и ВВ1, пересекаются по прямой. АВ1.
Соответственные углы при параллельных прямых и секущей равны. ⇒
∠АСС1= ∠АВВ1, ∠АС1С=∠АВ1В ⇒
∆ АСС1~∆ АВВ1 по первому признаку подобия треугольников.
Пусть коэффициент отношения отрезков АС:ВС будет а.
Тогда АВ=7а
Из подобия следует отношение:
АВ:АС=ВВ1:СС1
7:4=ВВ1:8
4 ВВ1=56⇒
ВВ1=14
5)
<DCK= 180°- (<CDK+<DKC) (тк сумма всех углов треугольника равна 180°)
<DCK= 180°- (28°+75°)=77°
<DKE= 180° - DKC (тк <DKE и <DKC - смежные)
<DKE= 180°-75°= 105°
<KDE= 28° (по рисунку)
<DEK= 180°- (<DKE+<KDE) (тк сумма всех углов треугольника равна 180°)
<DEK= 180°- (105°- 28°)= 47°
ответ: <DCK= 77°, <DKE= 105°, <KDE= 28°, < DEK= 47°
6)
В ^ABC стороны при основании равны => ^ABC равнобедренный => углы при основании равны.
1. 180°-40°= 140°
2. 140°:2°=70°
ответ: <A= 70°, <C= 70°
Объяснение:
обозначения :
< - угол
=> - следовательно
^ - треугольник
V=a3*√2/12=23*√2/12=8*√2/12=2√2/3=0,943