12 см²
Объяснение:
боковая сторона = (18 - 8) / 2 = 5 см
высота = 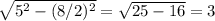 см
см
Площадь = 1/2 * 8 * 3 = 4 * 3 = 12 см²
Дано :
параллелограмм NPKA
<ANK = 45°
<KNP = 65°
Найти:
<А, <К, <Р, <N, <NKA, <NKP = ?
<N = <ANK + <KNP = 45° + 65° = 110°
<N = <K = 110° (св-во параллелограмма - противоположные углы равны)
<А = 180° - <К = 180° - 110° = 70° (свойство параллелограмма - углы, прилежащие к любой стороне, в сумме равны 180°)
<Р = <А = 70° (св-во параллелограмма - противоположные углы равны)
<NKA = <KNP = 65° (н.л. при NP//AK и секущей NK)
<NKP = <K - <NKA = 110° - 65° = 45°
ответ: <А = <Р = 70° ; <К = <N = 110° ; <NKA = 65° ; <NKP = 45°
У равнобедренного треугольника боковые стороны равны, вычислим их длину:
(18 - 8) : 2 = 10 : 2 = 5.
Вычислим площадь треугольника по формуле Герона:
S = √(р(p - a)(p - b)(p - c)), где р - это полупериметр треугольника, a, b и c - стороны треугольника.
Найдем полупериметр треугольника: р = 18 : 2 = 9.
Отсюда S = √(9 * (9 - 5)(9 - 5)(9 - 8)) = √(9 * 4 * 4 * 1) = 3 * 4 = 12.
ответ: 12