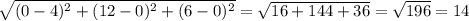Найдём высоту в трапеции по т.Пифагора зная гипотенузу 13 и катет 5(чтобы найти катет,опустили два перпендикуляра с верхнего основания и получили прямоугольник,а у прямоугольника противолежащие стороны равны,значит из нижнего основания вычитаем 10 и получаем 10,а так как трапеция равнобедренная то получившееся значение 10 делим на два и получаем 5) высота равна 13² - 5² = h² h = 12а дальше просто подставляем значения в формулу площади трапеции S = ((10 + 20)/2)*12 S = 180см²если что задавай вопросы
Боковая грань перпендикулярная основанию - равнобедренный треугольник с высотой Н = 12 см - высота пирамиды и разбивает грань на два прямоугольных треугольника с катетом Н = 12 см и острым углом 60
В прямоугольном треугольнике с катетом 12 см и противолежащим углом tg 60 =
a =
a = = 4√3 - половина стороны основания равностороннего треугольника
Площадь правильного треугольника (основания) со стороной 2а = 2 * 4√3 = 8 * 4√3 и высотой h = = √144 = 12
S = * 8√3 * 12 = 48√3 см²
Объем пирамиды с высотой H = 12 см и площадью основания S = 48√3 см²
(4;0;0) (0;12;6) 14
Объяснение:
Пусть т. А лежит на оси ОХ, тогда ее координаты будут (х;0;0)
Пусть т. В лежит в плоскости yz, тогда ее координаты будут (0;y;z)
Точка М (2; 6; 3) - середина отрезка АВ
AB =