ДАНО
c = 5 см - образующая конуса
D = 4 см - диаметр основания.
r= 1 см - диаметр шарика.
НАЙТИ
N =? - число шариков.
РЕШЕНИЕ
Объем конуса по высоте и радиусу основания по формуле:
V = 1/3*π*R²*H
Находим высоту конуса - H по теореме Пифагора.
b = R = D/2 = 4/2 = 2 см -
1) a² = 5² - 2² = 25 - 4 = 21
2) H = a = √21 - высота конуса.
Объем конуса
3) V1 = 1/3*π*4*√21= 4/3*√21*π см³ - объем конуса превращаем в шарики.
Объем шара по формуле - R = 1.
V2 = 4/3*π*R³ = 4/3*π
Находим число полученных шариков - делением.
N = V1 : V2 = √21 ≈ 4.6 ≈ 4 шт - шариков - ОТВЕТ
И еще 0,58 шарика останется
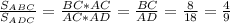
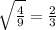 .
. 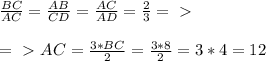
В Правильной четырёхугольный пирамиде боковое ребро образует с плоскостью основания угол 60° высота пирамиды равна 3 см. найдите объем пирамиды
Объяснение:
АВСМР-правильная пирамида.
V(пирам)=1/3*S(осн)*h.
S(осн)=S(квадрата)=0,5 АС² .
ΔАРО-прямоугольный , tg60=РО/АО ,√3=3/АО, АО=√3 см.
Вся диагональ АС=2√3 см. S(осн)=0,5 (2√3)²=2*3=6 (см²) .
V(пирам)=1/3*6*3 = 6 (см³).