
ABCD - прямоугольник.
AE ┴ ABCD.
ED = √7
EC = √8
EB = √6
Найти:АЕ - ?
Решение:Так как AD ┴ DC, AE ┴ABCD => ED ┴DC, по теореме о 3 перпендикулярах => △EDC - прямоугольный.
Найдём DC, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты).
DC = √(EC² - ED²) = √((√8)² - (√7)²) = √(8 - 7) = 1
У прямоугольника противоположные равны.
=> DC = AB = 1
Найдём АЕ, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты).
АЕ = √(EB² - AB²) = √((√6)² - 1²) = √(6 - 1) = √5.
Найдём АD, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)
AD = √(ED² - AE²) = √((√7)² - (√5)²) = √(7 - 5) = √2
AD = BC = √2 (у прямоугольника противоположные стороны равны)
S осн = S прямоугольника = a * b = AD * DC = AB * BC.
S прямоугольника = 1 * √2 = √2 ед.кв.
ответ: √2 ед.кв; √5 ед.изм.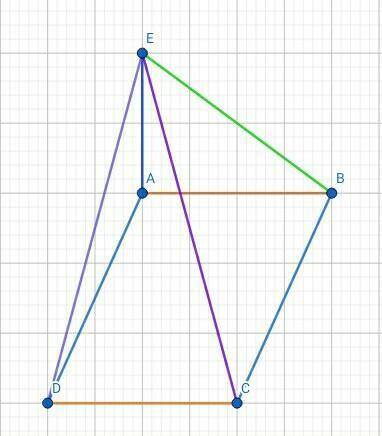
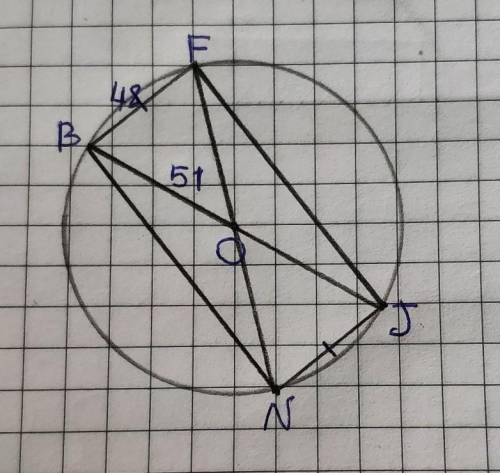
Исходя из того, что точки расположены на окружности: полученный четырехугольник будет вписан в окружность.
Так как противоположные стороны четырехугольника BF и NJ равны и паралельны друг другу по условию, то четырехугольник BFJN – параллелограмм.
Параллелограмм, который можно вписать в окружность – прямоугольник.
Проведём диагонали BJ и FN. Точка пересечения диагоналей, вписанного в окружность прямоугольника, является центром этой окружности, следовательно каждая диагональ является диаметром.
Тогда BJ – диаметр окружности.
Диаметр окружности вдвое больше её радиуса, получим что BJ=51*2=102 см.
Рассмотрим ∆BJF.
Так как BFJN – прямоугольник, то угол BFJ=90°, а ∆BJF – прямоугольный.
BJ=102 см,
BF=48 см по условию.
По теореме Пифагора в ∆BJF:
BJ²=BF²+FJ²
102²=48²+FJ²
FJ²=10404–2304
FJ=√8100
FJ=90 см.
Получим что другая сторона четырехугольника равна 90 см. Так как данный четырехугольник – прямоугольник, то противоположная ей сторона равна так же 90 см.
ответ: 90 см.
ответ и подробное решение на фото: