Question

Диагонали равносторонней трапеции перпендикулярны. Найти площадь трапеции, если ее основания равны 8 см и 20 см.​

Answer 1

Объяснение:

Если трапеция равнобедренная и диагонали перпендикулярны ,то высота равна средней линии.

h=m

m=(8+20):2= 14 см

S=hm=m²=14²= 196 см²

Answer 2

196см²

Объяснение:

1-ый

Соединим середины сторон трапеции. Если в равнобедренной трапеции соединить середины оснований, то, согласно замечательному свойству трапеции, на этом отрезке будет лежать точка пересечения диагоналей (это свойство нужно доказывать). Учитывая наше условие, получатся равнобедренные прямоугольные треугольники, откуда несложно понять, что высота будет равна средней линии. Тогда искомая площадь вычисляется по формуле 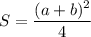$S=\dfrac{(a+b)^2}{4}$. Откуда получаем ответ 196см².

2-ой

Допустим, мы не увидели 1-ый В школе не всегда рассказывают замечательное свойство трапеции. Доказательство этого свойства достаточно интересное, поэтому до него можно не додуматься. Для такого случая есть 2-ой получения ответа.

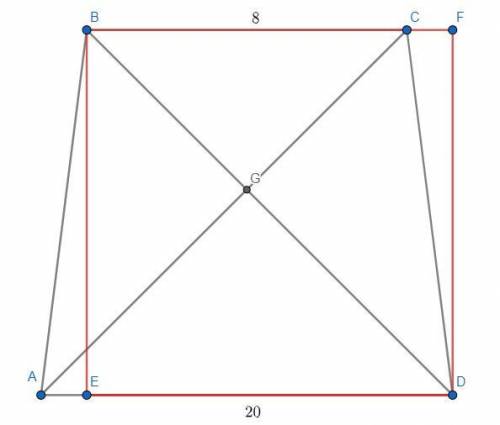
Проведем DF⊥BC. Тогда BEDF - прямоугольник или квадрат. Докажем, что площадь полученного четырехугольника равна площади трапеции и что этот четырехугольник квадрат.

Пусть 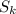$S_k$ - площадь нового четырехугольника, а 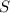$S$ - площадь трапеции.

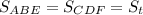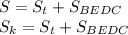
Заметим, что ΔABE=ΔCDF (AB=CD, так как трапеция равнобедренная, BE=DF - расстояния между параллельными прямыми равны и треугольники прямоугольные). Тогда $S_{ABE}=S_{CDF}=S_t$.

$S=S_t+S_{BEDC}\\S_k=S_t+S_{BEDC}$

Значит $S=S_k$

Значит четырехугольники равновеликие.

Перейдем ко 2-ому пункту доказательства:

Площадь произвольного четырехугольника, а, следовательно, и трапеции, вычисляется по формуле:

$S=\dfrac{1}{2}d_1d_2\times\sin\alpha$

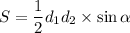
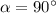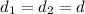По условию $\alpha=90^\circ$, а $d_1=d_2=d$, так как трапеция равнобедренная (можно доказать, что 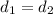$d_1=d_2$, из равенства треугольников ABC и BCD).

Тогда формула выше для нашего случая примет вид:

$S=\dfrac{d^2}{2}$

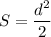
Четырехугольник BEDF содержит диагональ трапеции. И у прямоугольника, и у квадрата диагонали равны. Тогда пусть диагонали пересекаются под углом 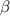$\beta$.

Получим:

$S_k=\dfrac{d^2}{2}\times\sin\beta$

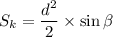
Выше говорилось, что $S=S_k$.

Значит:

$\dfrac{d^2}{2}=\dfrac{d^2}{2}\times\sin\beta\\\sin\beta=1\\\beta=90^\circ$

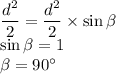
Тогда BEDF - квадрат. Значит высота трапеции равна его стороне.

Так, мы доказали, что площадь равнобедренной трапеции, диагонали которой перпендикулярны, вычисляется по формуле:

$S=\dfrac{a+b}{2}\times\left(a+\dfrac{b-a}{2}\right)=\dfrac{\left(a+b\right)^2}{4}$

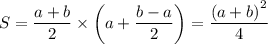
Воспользуемся ей, чтобы получить ответ:

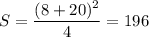$S=\dfrac{(8+20)^2}{4}=196$см².

Задача решена!