Не смотря на то, что эта задача есть в задачнике Прасолова, номер 18.7, с решением, я решил выложить свое решение. Метод тот же - векторный, но я немного отредактировал и условие и решение - по-моему, так понятнее.
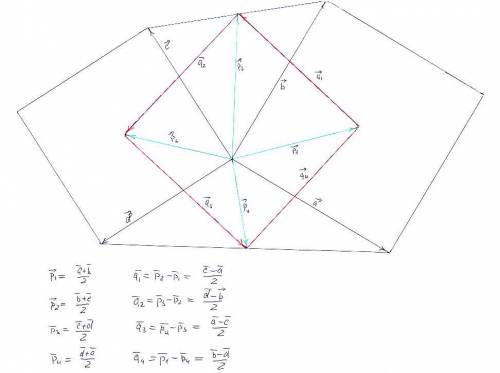
На вложенном чертеже показано, как вводится "базовая" четверка векторов - это две пары взаимно перпендикулярных и равных по величине векторов, то есть
lal = lbl; (или, то же самое, a = b, жирным отмечен вектор, а обычным шрифтом - его модуль);
ab = 0;
lcl =ldl; (c = d)
cd = 0;
На вложенном рисунке показано, как стороны искомой фигуры выражаются через эту четверку векторов. Уже очевидно, что эта фигура - параллелограмм.
Далее, угол между векторами a и d и угол между векторами c и b в сумме составляют 180°, поэтому ad = - cb;
Отсюда q1q4 = (c - a)(d - b)/4 = (-ad - cb)/4 = 0; угол между двумя сторонами - прямой, то есть эта фигура - прямоугольник.
Теперь надо показать, что соседние стороны равны по величине. Легко видеть, что
lq1l^2 = (c - a)^2/4 = (c^2 + a^2 - 2ac)/4;
lq2l^2 = (d - b)^2/4 = (d^2 + b^2 - 2db)/4;
Поскольку пара векторов a и c при повороте на 90° переходит в пару векторов b и d, то углы между этими парами векторов равны, то есть ac = bd,
(именно поэтому эта задача Прасоловым помещена в раздел " повороты на 90° ")
и q1 = q2 (модули!)
Это завершает доказательство того, что искомая фигура - квадрат.
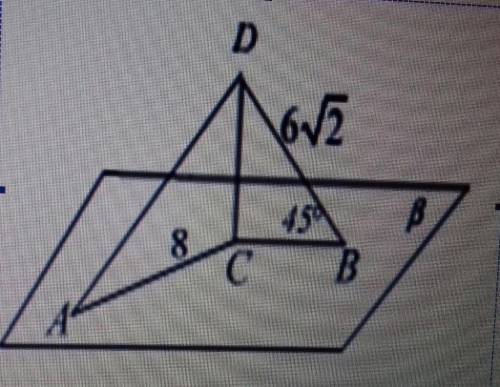
Пусть трапеции ABCD, где прямой угол - А.. Проведём высоту из т. С. Назовём её СО. Бис-са выходит из угла D. Тогда
1)угол DBC=BDA, Тк являбтся накрест лежащимт при прямых BC И AD И секущей BD. Тогда получается, что треуг BD равнобедренный.
2) в ранобедренном трег боковые стороны равны. BC=CD=15см.
3) рассмотрим прямоуг. ABCO. В прямоуг противолежсщие стороны равны. AB=CO=12, BC=AO=20.
4) рассмотрим треуг COD. По теореме Пифагора ОD^2= 225-144=81. Значит OD=9см.
5) AD=20+9=29см.
6) SABCD=(20+29)/2*12=39/2*12=39*6=234 СМ ^2