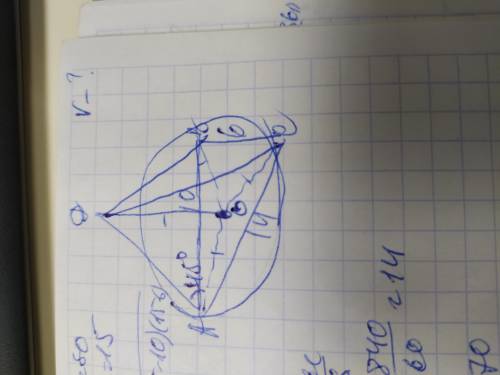
Обозначим вершины пирамиды АВС с высотой ДО. Объем пирамиды вычисляется по формуле: V=⅓×Sосн×ДО. Зная все стороны основания найдём его площадь через его полупериметр:
Р=14+10+6=30; Р/2=p=15дм
S=√((p(p-AC)(p-AB)(p-ВС))=
=√((15(15-14)(15-10)(15-6))=√(15×1×5×9)=
=√225=15дм²
S=15дм²
Опишем вокруг основания окружность с точкой О. АО=ВО=СО=R
R=AB×BC×AC/4S=14×10×6/4×15=840/60=
=14дм
Треугольники образуемые радиусами, высотой ДО и боковыми рёбрами - прямоугольные и так как боковые рёбра образуют с основанием угол 45°, то углы при вершине также будут 45°, поскольку сумма острых углов прямоугольного треугольника составляет 90°, и угол при вершине=90-45=45°, из чего следует что эти треугольники равнобедренные, поэтому радиус R=высоте ДО=14дм.
Теперь найдём объем пирамиды зная её высоту и площадь основания:
V=⅓×15×14=70дм³
ОТВЕТ: V=70дм³
ответ:
объяснение:
2. прямую можно обозначать одной маленькой латинской буквой (a,b,
или двумя заглавными латинскими буквами, если этими буквами обозначены точки, расположенные на прямой (ab, cd)
3. у прямой много свойств: через одну точку можно провести бесконечно много прямых, через любые две точки можно провести только одну прямую, у любой прямой, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие
4. прямые, лежащие в одной плоскости и имеющие одну общую точку, которую называют точкой пересечения прямых называют пересекающимися.
6. утверждение, имеющее доказательство, т.е. его надо доказать.
9. их тоже несколько (равные отрезки имеют равные длины, часть отрезка всегда имеет длину, которая меньше длины отрезка, если точки на отрезке делят отрезок на части, то длина отрезка равна сумме длин этих частей.
10. длина отрезка.
11.это точка, которая делит данный отрезок на две равные части.
70 dm3
Объяснение:
V=1/3*S*H - нужно найти высоту пирамиды и площадь основания. (1)
Так как каждое из боковых ребер наклонено к плоскости основания пирамиды под углом 45 градусов, то вершина пирамиды проецируется в центр описанной около основания окружности радиуса R.
Рассмотрим треугольник АВС , лежащий в основании и найдем R.
AB=6 dm, AC=10 dm, BC=14 dm
Тогда по т. косинусов запишем
196=36+100-2*6*10*cosA
120*cosA=-60
cosA=-1/2
A=120 градусов
Тогда sin A= sqrt(3)/2
Находим R по теореме синусов:
2R=BC/sinA= 14/sqrt(3)*2
R=14/sqrt(3)
Найдем высоту пирамиды:
h=R*tg45= 14/sqrt(3)
Найдем площадь основания по формуле:
S=АВ*AC*sinA/2= 6*10*sqrt(3)/2/2=15*sqrt(3) dm2
Тогда подставивив (1) h и S найдем обьем пирамиды:
V=1/3*15*sqrt(3)*14/sqrt(3)=5*14=70 dm3