ответ: 1)треугольник ABD=треугольник CBD по 1 признаку
2)MKP=треугольник NTK по 1 признаку
3)треугольник KPS=треугольник RKS по 2 признаку.
4)треугольник PRE=треугольник SKR по 2 признаку.
5)треугольник SPM=треугольникMKT по 1 признаку.
6)треугольник CED=треугольник FDC по 1 признаку.
7)треугольник MTR =треугольник STN по 2 признаку.
8)треугольник KNM =треугольник LMN по 2 признаку.
9)треугольник ADE = FMB треугольник по 2 признаку.
10)треугольник ADB = DBC треугольник по 1 признаку.
Объяснение:
Первый признак равенства треугольников: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников: Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Используя эти 3 признака можно легко понять как решить все эти задачи.
ответ: 24
Объяснение:
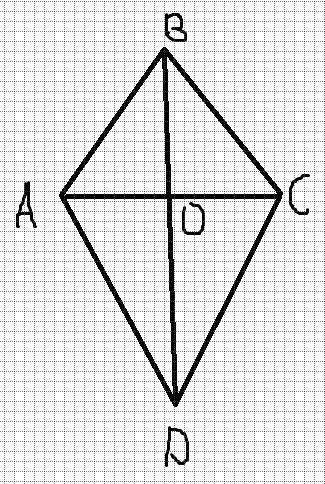
Смотри рисунок визуально становиться понятно что на против большее диагонали лежит больший угол то есть углы BAD=BCD=120 градусов, а так как углы ромба в сумме должны давать 360 и противоположные углы равны то углы ABC=CDA=60 градусов 360-240=120/2=60 из условия задачи мы знаем что AC=6 см. А еще у ромба есть такое свойство: Диагонали являются биссектрисами то есть углы ADO=ODC=ABO=OBC=30 градусов, а углы DAO=OAB=BCO=OCD=60 градусов соответственно. Есть такое своистово в прямоугольном треугольнике что напротив угла в 30 градусов располагается катет равный половине гипотенузы. Это свойство нам найти сторону ромба, а после зная сторону мы найдем периметр по формуле 4* на длинну стороны, кстати стороны у ромба равны вот. В нашем случае AO=1/2*AD так как AO лежит напротив угла прямоугольного треугольника AOD равного 30 градусов. Так как AD=DC=CB=AB, а углы DAC и ACD равны 60 градусов то треугольник ADC является равнобедренным. А у равнобедренных треугольников биссектриса, проведенная к основанию, является медианой и высотой. А так как угол AOD равен 90 градусов то OD есть не что иное, как высота биссектриса и медиана данного треугольника, а если она медиана то она делит AC пополам значит AO=6/2=3 значит AD=3*2=6, а периметр в итоге равен 6*4=24
Если в окружности хорда равна радиусу, то значит треугольник, образованный этой хордой и двумя радиусами, проведеннысм к концам хорды, образуют правильный трецгольник.
Строим правильный треугольник со стороной, равной АВ. Для этого на прямой "а" откладываем циркулем отрезок, равный данному и из концов А и В отрезка радиусами, равными АВ, делаем "засечки" по обе стороны от прямой "а". Соединив "засечки" с точками А и В отрезками, получаем два равносторонних треугольника со сторонами, равными АВ. Проведя окружности радиусами АВ с центрами в вершинах получившихся треугольников, имеем окружности, которые надо было построить.
Далее можно продолжать до бесконечности, строя окружности с центрами в точках пересечения полученных окружностей. У всех этих окружностей хорды и радиусы будут равны отрезку АВ.