Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
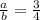, тогда а= 
.
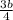По т. Пифагора а²+b²=(3+4)² ,( 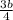)²+b²=49 ,
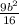+b²=49 , 9b²+16b²=49*16 , b²= 
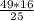, b=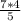
= 5,6 (см)
a=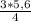 
=4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."
1)площадь ромба равна произведению его сторону на высоту (он же перпендикуляр между двумя противоположными сторонами)
сторону найдем через периметр
а=Р÷4=20÷4=5
в ромб вписана окружность. центр окружности расподожен на пересечении диагоналей ромба. если провести радиус от центра окружности к касательной (сторона ромба) то получим перпендикуляр. если провести такой же перпендикуляр к ротивоположной стороне, то получим высоту ромба, равную диаметру окружности
h=2R=2×2=4
s=ah=5×4=20
2) по теореме пифагора найдем вторую сторону прямоугольника
б=корень(c^2-a^2)=корень(20^2-12^2)=корень(400-144)=корень(256)=16
s=ab=12×16=192
3)найдем сторону квадрата
a=корень(s)=корень(64)=8
периметр
Р=4а=4×8=32
Решение в двух приложениях.
Объяснение: