Дан параллелограмм. Точки на двух соседних сторонах параллелограмма соединили с вершинами, как показано на картинке. Даны площади трёх серых частей, найдите площадь четвёртой серой части.
В пирамиде ABCD построим плоскости, перпендикулярные соответственно ребрам AB, AC и b>AD и проходящие через их середины. Эти плоскости будут равноудалены от точек A и B, A и C, A и D соответственно, поскольку геометрическим местом точек, равноудаленных от концов данного отрезка, является плоскость, проходящая через его середину и перпендикулярная ему. Обозначим точку пересечения этих плоскостей через O. Докажем, что эта точка существует и единственна. Действительно, две из этих плоскостей пересекаются по прямой l, поскольку они перпендикулярны двум непараллельным прямым. Эта прямая перпендикулярна к плоскости ABC. Плоскость, перпендикулярная AD, не параллельна l и не содержит её, поскольку в противном случае прямая AD перпендикулярна l, то есть лежит в плоскости ABC. Итак, точка O равноудалена от всех вершин треугольной пирамиды, значит эта точка является центром описанной сферы. Тем самым доказано существование такой сферы. Докажем теперь её единственность. Заметим, что центр любой другой сферы, проходящей через все вершины пирамиды, равноудален от всех этих вершин и, значит, принадлежит всем плоскостям, проходящим через середины ребер перпендикулярно последним. А это и означает, что центр такой сферы и точка O совпадают.
5. 28
6. 21
Объяснение:
5. АВ = 42, 2BC = AC - это если наше условие написать на математическом языке. Чтобы решить эту задачу, нужно составить уравнение
AC + BC = 42
Но чтобы у нас не было двух неизвестных, нужно один отрезок выразить через другой. Для этого мы и переписали условие
АС + BC = 2BC + BC
2BC + BC = 42
3BC = 42
BC = 42 : 3 = 14
Если BC = 14, то АС = 42 - 14 = 28.
6. АВ = 49, АС =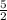
CB или 2,5СВ
Чтобы найти АС, мы переписали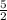
в 2,5 , чтобы проще было посчитать. АС - это две части и одна половинка этой части СВ. То есть,
СВ + СВ +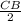
= AC.
СВ + СВ +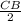
+ СВ = 49
3СВ +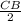
= 49, чтобы легко избавиться от некрасивой дроби, нужно две части уравнения домножить на 2
6СВ + СВ = 98
7СВ = 98
СВ = 14, следовательно АС = 49 - 14 = 35
Раз нам надо найти АС - СВ, то 35 - 14 = 21.