Question

в правильной треугольной пирамиде сторона основания 4√3 см. Боковое ребро наклонено к плоскости и основанию под углом 30 градусов. Найти объем пирамиды​

Answer 1

$V = 8\sqrt{15}$

Объяснение:

(Смотри вложение)

Формула объёма пирамиды: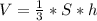 $V = \frac{1}{3}*S*h$ , где:

S - площадь основания

h - высота пирамиды

Т.к. пирамида правильная ⇒ в основании лежит правильный многоугольник, то есть, в нашем случае, равносторонний треугольник

Формула площади треугольника: SΔ =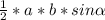 $\frac{1}{2} * a * b * sin\alpha$, где

а - одна сторона

b - соседняя с а сторона

sin α - синус угла между сторонами a и b

Т.к. в основании треугольник равносторонний⇒все углы = 60° и a=b

SΔ =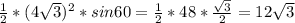 $\frac{1}{2} * (4\sqrt{3})^{2} * sin 60 = \frac{1}{2} * 48 * \frac{\sqrt{3} }{2} = 12\sqrt{3}$

Рассмотрим ΔABC

Т.к. все треугольники равносторонние (т.к. пирамида правильная) ⇒ высота AD является также медианой и биссектрисой. Получается ∠ABC =∠ACB = 60° : 2 = 30°  и BD=DC = 4√3 : 2 = 2√3

Рассмотрим ΔADC

По т. Пифагора

AD = √AB²-BD²

AD = √(4√3)²-(2√3)² = √48 - 12 = √36 = 6

Высота пирамиды опускается в точку пересечения биссектрис основания, поэтому HD =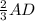 $\frac{2}{3} AD$ = 4 (Т.к. биссектрисы в точке пересечения делятся 1:2 считая от вершины)

Т.к. все треугольники равносторонние ⇒ высоты у каждого треугольника пирамиды равны, то есть AD = SD

Рассмотрим ΔSHD

ΔSHD - прямоугольный, т.к. SH - высота

По т. Пифагора

SH = √SD²-HD²

SH = √6²-4² = √36-16 = √20 = 2√5

Теперь нам известны все данные для нахождения объёма пирамиды.

$V = \frac{1}{3}*12\sqrt{3} *2\sqrt{5} = 8\sqrt{15}$