ответ:Геометрический смысл φ ясен из рис. 125. Отрезок прямой разделен на два отрезка А и В, которые, как говорят, образуют "золотое сечение" отрезка А + В: длина всего отрезка (А + В) находится в таком же отношении к длине отрезка А, как и длина отрезка А к длине отрезка В. Отношение каждой пары отрезков и равно числу φ. Если длина отрезка В равна 1, то значение φ нетрудно вычислить из уравнения
которое можно записать в виде обычного квадратного уравнения А2 - А - 1 = 0. Положительный корень этого уравнения равен
Это число одновременно выражает длину отрезка А и значение величины φ. Его десятичное разложение имеет вид 1,61803398... Если за единицу принять длину А, то длина В будет выражаться величиной, обратной φ, то есть 1/φ. Любопытно, что 1/φ = 0,61803398... Число φ - единственное положительное число, которое переходит в обратное ему при вычитании единицы.
Подобно числу π, φ можно представить в виде суммы бесконечного ряда многими Предельная простота следующих двух примеров еще раз подчеркивает фундаментальный характер φ:
ответ: 8.5
Объяснение:
Заметим, что точка не лежит между двумя параллельными прямыми, а значит, фигура которая высекается прямыми будет трапецией в плоскости АD1D2, так как прямые параллельны. Посмотрим на рисунок в плоскости АD1D2 - это, как уже было сказано ранее, трапеция, но не простая. Известно равенство отрезков KC1 = C1D1. Рассмотрим ΔD1D2K.
В нем проведена прямая С1С2 ║основанию через середину стороны D1K(KC1 = C1D1), значит эта прямая - средняя линия треугольника ⇒точка C2 делит сторону пополам и, по свойству средней линии,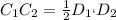 
. Находим по этой формуле C1C2. Он равен 8.5.
7,66 ед2
Решение задачи прилагаю