

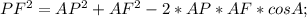
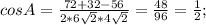
 ,
, 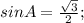

Какое из следующих утверждений верно?
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
ЗАДАНИЕ №2.
Какое из следующих утверждений верно?
1) Треугольника со сторонами 1, 2, 4 не существует.
ЗАДАНИЕ №3.
Какие из следующих утверждений верны?
3) Все диаметры окружности равны между собой.
ЗАДАНИЕ №4.
Какое из следующих утверждений верно?
1) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
ЗАДАНИЕ №5.
Укажите номера верных утверждений.
1) Любые три прямые имеют не более одной общей точки.
3) Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.
ЗАДАНИЕ №6.
Укажите номера неверных утверждений.
1) При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.
3) Если угол равен 47°, то смежный с ним равен 153°.
ЗАДАНИЕ №7.
Укажите номера верных утверждений.
2) Любые две прямые имеют ровно одну общую точку.
3) Если угол равен 108°, то вертикальный с ним равен 108°.
ЗАДАНИЕ №8.
Какие из данных утверждений верны? Запишите их номера.
2) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
3) Через любые две точки можно провести прямую.
ЗАДАНИЕ №9.
Укажите номера верных утверждений.
1) Через любую точку проходит не менее одной прямой.
2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
ЗАДАНИЕ №10.
Какие из следующих утверждений верны?
2) Если угол равен 60°, то смежный с ним равен 120°.
3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
ЗАДАНИЕ №11.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) Сумма смежных углов равна 180°.
ЗАДАНИЕ №12.
Укажите номера верных утверждений.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Обозначим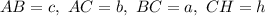 . Пусть
. Пусть 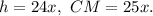 Поскольку
Поскольку 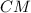 — медиана, то
— медиана, то 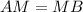 и так как
и так как 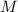 — центр описанной окружности, то
— центр описанной окружности, то 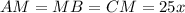 (как радиусы окружности). Тогда
(как радиусы окружности). Тогда 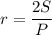 , площадь треугольника
, площадь треугольника 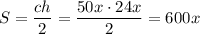 кв.ед. Определим теперь периметр:
кв.ед. Определим теперь периметр:
Радиус вписанной окружности: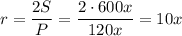 .
.
Определим теперь отношение радиусов описанной и вписанной окружностей.
ответ: R : r = 5 : 2.