Question

Гипербола, у которой асимптоты являются координатными осями и прямая с уравнением 3x-4y-12=0 является касательной, имеет уравнение: ответ: xy+3=0
Как решить?

Answer 1

Преобразуем уравнение прямой в явный вид

$3x-4y-12=0 = -4y=12-3x = y=\frac{3}{4}x-3$

Так как асимптотами гиперболы являются координатные оси, ее уравнение можно представить в виде

$y=\frac{a}{x}$ где а - некоторый параметр, его мы и будем искать.

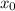Пусть $x_0$ - точка касания, тогда справедливо следующее

- значение неизвестной функции в точке касания и прямой совпадают

$\frac{a}{x_0}=\frac{3}{4}x_0-3$

- значение производной в точке касания совпадает с угловым коэффициентом прямой

$-\frac{a}{x_0^2}=\frac{3}{4}$

Эти два уравнения образуют систему, разрешим ее относительно параметра а

$a=-\frac{3}{4}x_0^2$

$-\frac{3}{4}x_0^2\frac{1}{x_0}=\frac{3}{4} x_0-3$

$-\frac{3}{4}x_0=\frac{3}{4}x_0-3$

$-\frac{3}{2}x_0=-3 = x_0=2$

Тогда параметр а

$a=-\frac{3}{4}*2^2=-3$

Значит, уравнение гиперболы имеет вид

$y=-\frac{3}{x}$

Или, в неявной форме

$xy=-3 = xy+3=0$

Что и требовалось доказать.